Real and imaginary parts for $F(\varphi,m)$ with complex argument

Question

I have this case: $F(\arcsin u,m)$, where $u>1$, so it ends up as $F(\frac{\pi}{2}-i\text{arccosh} u,m)$.

and I need to decompose it into real and imaginary parts. I have seen this question, but it has no answer. After some searches, looking through Abramowitz & Stegun, at 17.4.11 it describes how to do that:

$$F(\phi+i\psi,m)=F(\lambda,m)+iF(\mu,m)$$

where $\cot^2\lambda$ is the positive root of

$$x^2-\left[\cot^2\phi+m\sinh^2\psi\csc^2\phi-m_1\right]x-m_1\cot^2\phi=0\tag{1}$$

and

$$m\tan^2\mu=\tan^2\phi\cot^2\lambda-1\tag{2}$$

It turns out that the real part ends up as the complete elliptic integral of the first kind, $F(\lambda,m)=K(m)$, which suits me just fine, so all I have to do is determine the imaginary part, which means I need $\mu$, which derives from $\lambda$. For my case $\phi=\frac{\pi}{2}\Rightarrow \cot^2\phi=0,\space\csc^2\phi=1$, so $(1)$ becomes:

$$x^2-\left[m\sinh^2(\text{arccosh}u)-m_1\right]x-m_1=0$$

so, considering that $m<0.1$ (practical values are $0.01$ or less), gives the positive root (with the help of wxMaxima, I'm not versed in math):

$$\lambda_+=\frac{\sqrt{m^2(u-1)^2(u+1)^2+m_1\left[2m(1-u^2)+4\right]+m_1^2}+m(u^2-1)-m_1}{2}$$

So far, so good, but now I have problems in expressing $\mu$ from $(2)$:

$$\mu=\arctan\left(\frac{\sqrt{\tan^2\phi\cot^2\lambda-1}}{m}\right)$$

Did I do it right so far? If yes, what do I do with $\tan\phi=\tan\left(\frac{\pi}{2}\right)$? If not, how should I proceed?

---

Looking in the same A&S, section 17.4.8 describes the transforming of the completely imaginary argument:

$$F(i\phi,m)=iF(\theta,1-m),\space\theta=\arctan(\sinh\phi)$$

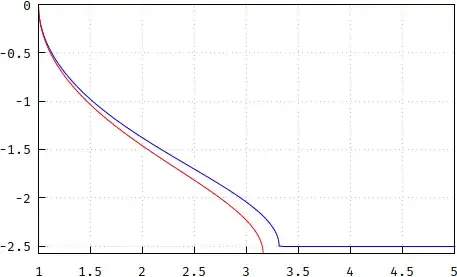
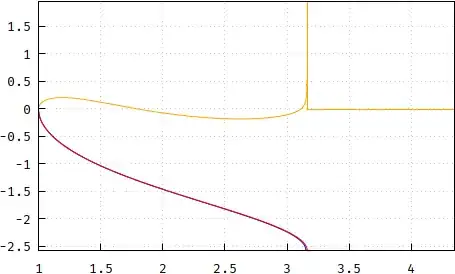
Knowing that the $\lambda$ calculated earlier is different than the $\mu=\text{arccosh}u$, I still tried plotting $F(\arctan(\sinh(\text{arccosh}u)),1-m)$ (got curious), where the argument reduces to (thanks to wxMaxima) $\arctan\sqrt{u^2-1}$. By mistake, I wrote $1+m$ in the modulus, instead of $1-m$, and this came up for $m=0.1$:

and for $m=0.01$, which is about the maximum value $m$ can take in my application:

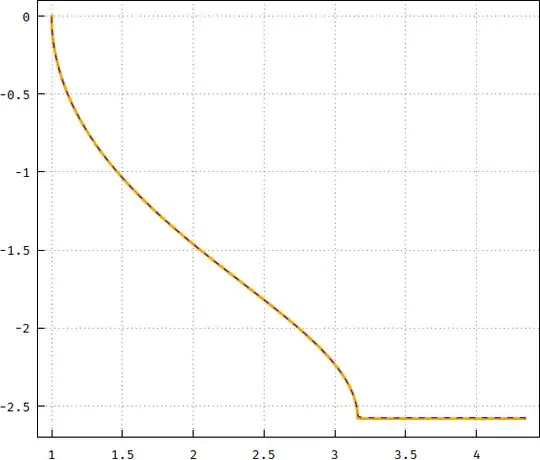
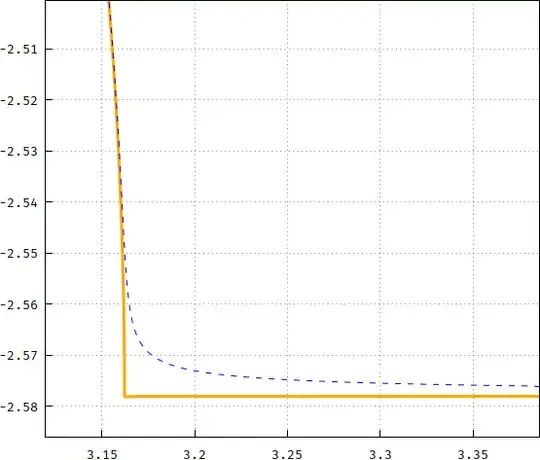
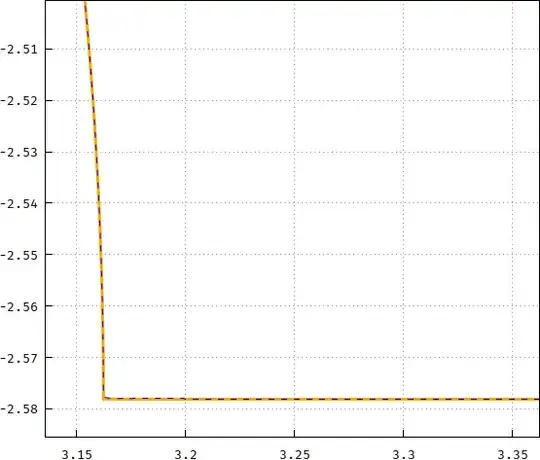
Not only it gets closer, but for $m=0.1$ I used the hammer to tweak the modulus and the exponent to be something like $F(\arctan\sqrt{u^{2.2}-1},0.98625+m)$, and the result is this (the difference is in orange, multiplied by 100):

Is this a known "shortcut"? Is this worth following?

Answer 1

There are in fact two sets of formulas for $F(\sin^{-1}u,m)$ with $u>1$, depending on whether $u>\frac1{\sqrt m}$ or not. Both are very simple and don't have the problem of the tangent blowing up at $\pi/2$.

If $1\le u\le\frac1{\sqrt m}$, Byrd and Friedman 115.02 gives $$F(\sin^{-1}u,m)=K(m)+iF\left(\sin^{-1}\frac{\sqrt{u^2-1}}{u\sqrt{1-m}},1-m\right)$$ If $\frac1{\sqrt m}\le u$, Byrd and Friedman 115.03 gives $$F(\sin^{-1}u,m)=F\left(\sin^{-1}\frac1{u\sqrt m},m\right)+iK(1-m)$$

Answer 2

I found an answer that may not be entirely orthodox, and is not 100% accurate, but 99.999...%, depending on the accepted tolerance, due to circumventing the $\tan\frac{\pi}{2}$ term.

First, there are some errors in the OP, mostly due to me not knowing how to properly read the spartan (to me) explanations in the Abramowitz & Stegun book, and some due to misreading. I'll correct them here, rather than in the OP, since it might get messy, and maybe change the question(?).

1. In the first decomposition equation, the imaginary term in the right side has $m_1=1-m$ as modulus.
2. The simplified equation $(1)$ should not have the last, single $m_1$ term due to $cot^2\phi=0$. Still, this step should not be performed (explained below).
3. The square root in the expression of $\mu$ encompasses the denominator, too.

Another mistake was considering $\lambda$ as the root and extracting it from $\cot^2\lambda$ -- this should not be done as the whole root is considered as $\cot^2\lambda$. So now the steps are these:

1. Solve equation $(1)$ for the positive root and assign it to (I hope I made no mistake):

$$\begin{align}\lambda=&\frac{(\csc^2\phi\sinh^2\psi+1)m+\cot^2\phi-1}{2}+\\ &+\frac{\sqrt{2m\csc^2\phi\sinh^2\psi(m+\cot^2\phi-1)+m^2(\csc^4\phi\sinh^4\psi+1)-2m(\cot^2\phi-1)+(\cot^2\phi+1)^2}}{2}\end{align}$$

2. Calculate $\mu$ as:

$$\mu=\arctan\sqrt{\frac{\lambda\tan^2\phi-1}{m}}$$

3. Now extract $\lambda$ and write the result as:

$$F(\phi+i\psi,m)=F(\arctan\sqrt{\lambda},m)+iF(\mu,1-m)$$

A quick test in wxMaxima with some random numbers $\phi=0.618$ and $\psi=i1.618$ gives ((%o8) being the true result):

(%o8)   1.583458041359163*%i+0.5015963344206276
(%o9)   1.583458041359162*%i+0.5015963344206277

This is for the general case. For my particular case, $\phi=\pi/2$ so the first caveat is circumventing the undefined tangent by simply making $\phi=\pi/2.001$, or similar (or simply discard the tangent term and write instead $1000$ or higher), which brings the second caveat, as mentioned in the 2nd error: simplifying should not be done as that changes the roots(!). Which means that the whole solution is quite fluffy when you consider implementing it in C++ (which is what I need).

Still, the $\text{arccosh}$ can be simplified by considering:

$$\begin{align}\psi&=\text{arccosh}u\\ \sinh\psi&=\sinh(\text{arccosh}u)=\sqrt{u^2-1}\\ \sinh^2\psi&=u^2-1\space\Rightarrow\end{align}$$

which results in the root

$$\begin{align}\lambda=&\frac{\csc^2\phi(u^2-1)m+m+\cot^2\phi-1}{2}+\\ &+\frac{\sqrt{2m(u^2-1)\csc^2\phi(m+\cot^2\phi-1)+(\csc^2\phi(u^2-1)m)^2+m(m-2)+\cot^2\phi(2-2m+\cot^2\phi)+1}}{2}\end{align}$$

with $\mu$ as above. Plotting the function now takes a second or two (for my case it only needs to be evaluated in one point), but here's how it looks:

The orange trace is the correct one, the blue, dashed one is this approximation. Due to the circumvention, a minor curve can be seen below, at the sharp knee. Here's a zoom:

Adding two more zeroes to $\phi=\pi/2.00001$ results in a much better result:

This is done in double precision, no Maxima big floats (bfloat). I think it's safe to say this is a good way to do it.