There are various known 3D Rep-Tiles and Irreptiles. Almost all of them are based on polycubes OR 2D reptiles. What are the 3D rep-tiles and irreptiles not based on polycubes and 2D reptiles?
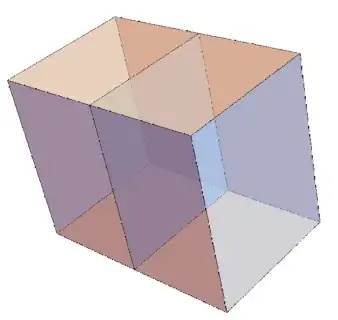
One infinite set uses $n$ bricks of size $(r^0,r^1,r^2)$ where $r=\sqrt[3]{n}$. The Delian Brick uses two bricks based on the Delian constant.
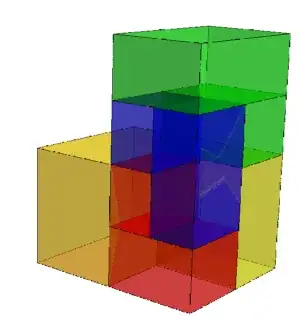
The first to use the Delian brick may have been Thickfun and Dale Walton, who expanded this into the Fifth Chair puzzle, a 4-irreptile.
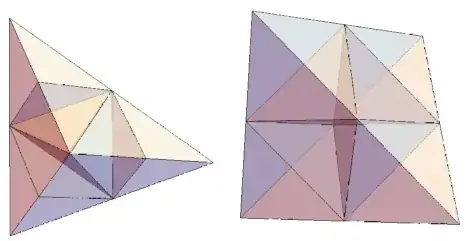
Of the five space-filling tetrahedra, at least two are 8-reptiles.
I've put together code for all of these. Are there any other 3D shapes which can be self-divided into smaller similar shapes, where the underlying shape is not a 2D reptile or a polycube?