Cool way of finding $\cos\left(\frac{\pi}{5}\right)$

Question

while trying to solve a problem, I stumbled upon a way of finding $\cos\left(\frac{\pi}{5}\right)$ using identities and the cubic formula. Is it possible to find other values of sine or cosine in a similar way ?

Consider $$\cos\left(\frac{\pi}{5}\right) - \cos\left(\frac{2\pi}{5}\right).$$ Using the difference of cosines identity, we have $$\cos\left(\frac{\pi}{5}\right) - \cos\left(\frac{2\pi}{5}\right) = -2\sin\left(\frac{3\pi}{10}\right)\sin\left(-\frac{\pi}{10}\right).$$

Now we change the RHS using the identity $\sin(x) = \cos\left(\frac{\pi}{2}-x\right)$ and the fact that $\sin(x)$ is odd.

$$-2\sin\left(\frac{3\pi}{10}\right)\sin\left(-\frac{\pi}{10}\right) = 2\cos\left(\frac{\pi}{5}\right) \cos\left(\frac{2\pi}{5}\right)$$ So, $$\cos\left(\frac{\pi}{5}\right) - \cos\left(\frac{2\pi}{5}\right) = 2\cos\left(\frac{\pi}{5}\right) \cos\left(\frac{2\pi}{5}\right)$$

Now we make use of the identity $\cos(2x)=2\cos^2(x)-1$. $$\cos\left(\frac{\pi}{5}\right) - 2\cos^2\left(\frac{\pi}{5}\right)+1 = 2\cos\left(\frac{\pi}{5}\right) \left(2\cos^2\left(\frac{\pi}{5}\right)-1\right)$$ Let $y=\cos\left(\frac{\pi}{5}\right)$ and we have $$y-y^2+1=2y(2y^2-1)$$ $$4y^3+2y^2-3y-1=0$$ which has the correct solution $$ y=\frac{\sqrt{5}+1}{4} =\cos\left(\dfrac{\pi}{5}\right) $$ One of the roots is also $\sin\left(\dfrac{\pi}{10}\right)$ which I'm guessing is because you end up with the same cubic if you apply the above to sin too.

Answer 1

Using complex numbers we can derive $\sin(\frac{\pi}{5})$ and $\cos(\frac{\pi}{5})$ $$ z^5=-1 \implies z^4-z^3+z^2-z+1=0 \implies z^2+\frac{1}{z^2}-z-\frac{1}{z}+1=0 $$ By substitution $t=z+\frac{1}{z}$ we get: $$ t^2-t-1=0 \implies t=\frac{1\pm\sqrt{5}}{2} $$ And because $\cos(\frac{\pi}{5})$ is positive, we may consider just $t=\frac{1+\sqrt{5}}{2}$

$$ z^2-z\frac{1+\sqrt{5}}{2}+1=0 \implies z=\frac{1+\sqrt{5}}{4}\pm i\frac{\sqrt{10-2\sqrt{5}}}{4} $$ And we get that $\cos(\frac{\pi}{5}) = \frac{1+\sqrt{5}}{4} $ and $\sin(\frac{\pi}{5})= \frac{\sqrt{10-2\sqrt{5}}}{4}$

Answer 2

There is a slightly shorter way:

$$\sin\frac{\pi}{5}=\sin\frac{4\pi}{5}=2\sin\frac{2\pi}{5}\cos\frac{2\pi}{5}=4\sin\frac{\pi}{5}\cos\frac{\pi}{5}\cos\frac{2\pi}{5}$$

Hence

$$\cos\frac{\pi}{5}\cos\frac{2\pi}{5}=\frac14$$

You can also write this

$$\cos\frac{\pi}{5}\cos\frac{3\pi}{5}=-\frac14$$

Then, using the formula $2\cos a\cos b=\cos(a+b)+\cos(a-b)$, you have:

$$\frac12=2\cos\frac{\pi}{5}\cos\frac{2\pi}{5}=\cos\frac{\pi}{5}+\cos\frac{3\pi}{5}$$

Hence $\cos\frac{\pi}{5}$ and $\cos\frac{3\pi}{5}$ are the roots of $t^2-\frac12t-\frac14$. The rest is easy, and the positive root is $\cos\frac{\pi}5$.

---

To answer your question: in general, it's not possible to find values of $\cos\frac{\pi}{n}$ only by radicals, even though they are algebraic numbers. Even in the case you obtain an irreducible cubic equation (which can be solved by radicals), it's the "trigonometric case" here, which has no expression with real radicals (and a complex cubic root needs the trigonometric functions anyway). For instance, $\cos1^\circ$ can't be computed with real radicals. But $\cos3^\circ$ can.

Even if in general it's not possible, there are a few tricks you can apply, for instance

$$\cos\frac{\pi}{12}=\cos\left(\frac{\pi}{3}-\frac{\pi}{4}\right)$$

Also, if you can compute $\cos x$ by radicals, then you can compute $\cos\dfrac{x}{2^n}$ too.

---

So, which angles of the form $\frac{\pi}{n}$ leads to trigonometric functions computable by radicals? The answer is given by the Gauss-Wantzel theorem. For instance, one can compute $\cos\dfrac{\pi}{17}$. However, the computation is not obvious, see http://mathworld.wolfram.com/TrigonometryAnglesPi17.html

Answer 3

Not so cool. The following may be cooler.

Let $\Delta ABC$ be a triangle with $\angle BAC=36^o$, $\angle ABC=\angle ACB=72^o.$ $BD$ bisects $\angle ABC$. $BE\perp AC$. You would find that $AD=BD=BC$ and $\Delta ABC \sim \Delta BDC.$ Thus, as the figure shows, we may obtain $$\frac{x}{2y}=\frac{x+2y}{x}.$$ Thus $$\left(\frac{x}{y}\right)^2-2\left(\frac{x}{y}\right)-4=0.$$

Solve it. We have $$\frac{x}{y}=1+\sqrt{5}.$$

Another negative root is not what we want.Thus, $$\cos 36^o=\frac{AE}{AB}=\frac{x+y}{x+2y}=\dfrac{\dfrac{x}{y}+1}{\dfrac{x}{y}+2}=\frac{1+\sqrt{5}}{4}.$$

Answer 4

Everything begins with finding $\sin\left(\frac{\pi}{10}\right)$

Okay... Lets say $x=\frac{\pi}{10}$

$$5x=\frac{\pi}{2}$$ $$2x=\frac{\pi}{2}-3x$$ $$\sin(2x)=\sin\left(\frac{\pi}{2}-3x\right)$$ $$\sin(2x)=\cos(3x)$$ $$2\sin(x)\cos(x)=4\cos^3(x)-3\cos(x)$$ $$2\sin(x)\cos(x)-4\cos^3(x)+3\cos(x)=0$$ $$\cos(x)\left(2\sin(x)-4\cos^2(x)+3\right)=0$$ $$2\sin(x)-4\cos^2(x)+3=0$$ $$2\sin(x)-4(1-sin^2(x))+3=0$$ $$2\sin(x)-4+4\sin^2(x)+3=0$$ $$4\sin^2(x)+2\sin(x)-1=0$$ Now use the formula $x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$ $$a=4,b=2,c=-1$$ $$=\frac{-2\pm \sqrt{2^2-4(4)(-1)}}{2(4)}$$ $$=\frac{-2\pm \sqrt{20}}{8}$$ $$\sin\left(\frac{\pi}{10}\right)=\frac{-1\pm \sqrt{5}}{4}$$

One another way of finding the value of $\cos\left(\frac{\pi}{5}\right)$

$$\cos\left(\frac{\pi}{5}\right)=\cos\left(2\left(\frac{\pi}{10}\right)\right)$$ $$=1-2\left(\sin\frac{\pi}{10}\right)^2$$ Since $\sin\left(\frac{\pi}{10}\right)=\frac{\sqrt{5}-1}{4}$ $$=1-2\left(\frac{\sqrt{5}-1}{4}\right)^2$$ $$=1-\frac{(\sqrt{5}-1)^2}{8}$$ $$=\frac{8-5-1+2\sqrt{5}}{8}$$ $$=\frac{2+2\sqrt{5}}{8}$$ $$\cos\left(\frac{\pi}{5}\right)=\frac{1+\sqrt{5}}{4}$$ Now lets find $\sin\left(\frac{\pi}{5}\right)$ $$\sin\left(\frac{\pi}{5}\right)=\sqrt{1-\cos^2\left(\frac{\pi}{5}\right)}$$ $$=\sqrt{1-\left(\frac{1+\sqrt{5}}{4}\right)^2}$$ $$=\sqrt{1-\frac{1+5+2\sqrt{5}}{16}}$$ $$=\sqrt{\frac{10-2\sqrt{5}}{16}}$$ $$\sin\left(\frac{\pi}{5}\right)=\frac{\sqrt{10-2\sqrt{5}}}{4}$$

Answer 5

Here is what I would describe as an intuitive (and therefore cool) method for calculating $\cos\left(\frac{\pi}{5}\right)$. It is logically very similar to the answer provided by mengdie1982, but I have tried to make the explanation more intuitive. First I will describe a special type of triangle, then I will derive the ratio of lengths in this triangle. I will then prove that one of the angles in this triangle is $\frac{\pi}{5}$, and finally it will be easy to calculate $\cos\left(\frac{\pi}{5}\right)$ from the previously calculated ratio of lengths. I will also explain how this special triangle can be constructed.

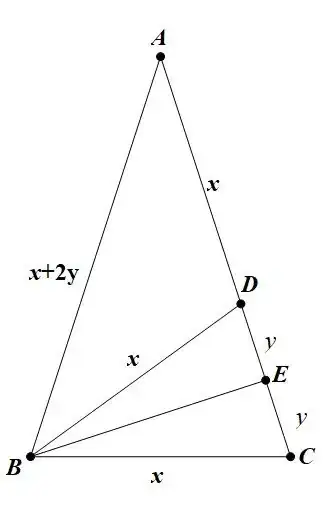
Consider the following triangle:

We have $\vert AB\vert = \vert BC \vert = a$ (so $\triangle ABC$ is isosceles), $\vert AC\vert = \vert CD \vert = b$ (so $\triangle ACD$ is also isosceles), $E$ is the midpoint of $AC$, and $F$ is the midpoint of $AD$.

What must be the ratio $\frac a b$ such that $\triangle BCD$ is also isosceles (IE such that $\vert BD\vert = \vert CD \vert = b$)?

Define $\angle ABE = \theta$,

$$ \Rightarrow \angle BAE = \frac \pi 2 - \theta \\ \Rightarrow \angle ACF = \theta \\ a\sin(\theta) = \frac b 2 \\ b\sin(\theta) = \vert AF \vert = \vert DF \vert \\ \vert AF \vert + \vert DF \vert + \vert BD \vert = a \\ \vert BD \vert = b \Rightarrow 2b\sin(\theta) + b = a \\ \Rightarrow \frac{b^2}{a} + b = a \\ \Rightarrow \frac{a + b}{a} = \frac a b $$

So, we have that if the isosceles triangle $\triangle ABC$ can be divided into 2 smaller isosceles triangles $\triangle ACD$ and $\triangle BCD$, then $\frac a b$ is the golden ratio!

We can solve for $\frac a b$ and then calculate $\sin(\theta)$:

$$ \left(\frac a b\right)^2 - \frac a b - 1 = 0 \\ \Rightarrow \left(\frac a b - \frac 1 2\right)^2 - \frac 5 4 = 0 \\ \Rightarrow \frac a b = \frac{1 \pm \sqrt{5}}{2} \\ \frac a b > 0 \Rightarrow \frac a b = \frac{1 + \sqrt{5}}{2} \\ \Rightarrow \sin(\theta) = \frac{b}{2a} = \frac{1}{1 + \sqrt{5}} $$

But what is the angle $\theta$? We can use the fact that $\triangle BCD$ is isosceles $\Rightarrow \angle BCD = \angle CBD = 2\theta$

$$ \angle ABE = \theta \Rightarrow \angle ACB = \frac \pi 2 - \theta \\ \angle ACB = \angle ACF + \angle DCF + \angle BCD \\ \Rightarrow \frac \pi 2 - \theta = \theta + \theta + 2\theta \\ \Rightarrow \theta = \frac{\pi}{10} \\ \Rightarrow \cos\left(\frac \pi 5\right) = \cos\left(2 \frac{\pi}{10}\right) = \cos(2\theta) = 1 - 2\sin(\theta)^2 \\ = 1 - \frac{2}{(1 + \sqrt{5})^2} = 1 - \frac{2}{6 + 2\sqrt{5}} = \frac{4 + 2\sqrt{5}}{6 + 2\sqrt{5}} \\ = \frac{(4 + 2\sqrt{5})(6 - 2\sqrt{5})}{(6 + 2\sqrt{5})(6 - 2\sqrt{5})} = \frac{4 + 4\sqrt{5}}{16} \\ = \frac{1 + \sqrt{5}}{4} $$

There you have it.

Because the sides of $\triangle ABC$ are in the golden ratio, $\triangle ABC$ is known as a golden triangle. It is straightforward to construct a golden triangle. Say you have already constructed a golden rectangle, which is upright, as shown below. Draw a circle with centre at the bottom left corner and radius equal to the width of the rectangle, and another circle with centre at the top left corner and radius equal to the height of the circle. Draw a triangle with corners at (either) intersection of these 2 circles and the centre of each circle. This is an isosceles triangle whose lengths are in the golden ratio (and with 2 long sides and one short side), so this is a golden triangle. :)