Given $\sin{x} = \frac{1 + \sqrt{5}}{4}$, find $x$

Question

If I have been given that $$\sin{x} = \frac{1 + \sqrt{5}}{4}$$ is there any way using which I can find out what the value of $x$ is? Sure I can remember the values, but I was curious whether if I knew the values of $\sin{\frac{\pi}{2}}, \sin{\frac{\pi}{4}}, \sin{\frac{\pi}{3}}$ I could somehow figure out what $x$ would be? Is there any intuition behind it?

Answer 1

Here is a tricky way to get at the solution without "knowing" it.

Start with $\sin x =(\sqrt5+1)/4$. Convert this to a quadratic equation by identifying the conjugate $(-\sqrt5+1)/4$ as the other root. Then since the sum of these two roots is $1/2$ and the product is $-1/4$, we identify the quadratic equation

$4\sin^2x-2\sin x-1=0$

Now multiply by $\cos x$ and apply the double angle formula $\sin 2x=2\sin x\cos x$:

$2\sin x\sin2x-\sin 2x-\cos x=0$

And now apply the sum-product relation $2\sin u\sin v =\cos (u-v)-\cos(u+v)$ (be careful with signs!), and note what happens to the $\cos x$ term: $\require{cancel}$

$\cancel{\cos x}-\cos 3x-\sin 2x\cancel{-\cos x}=0$

$\color{blue}{\cos 3x=-\sin 2x}$

So, from the complementary angle relations we must have one of the following:

$\color{blue}{3x+2x=(4n+3)\pi/2,n\in\mathbb{Z}}$

$\color{brown}{3x-2x=(4m+1)\pi/2,m\in\mathbb{Z}}$

If $x$ is to be a positive quantity strictly between $0$ and $\pi/2$ (radians), then only the first of these two relations gives a solution and it matches the required range only for $n=0$! Thereby $\color{blue}{x=3\pi/10}$ is selected among arguments between $0$ and $\pi/2$.

It is instructive to plot the solutions to the two complementary-angle relations.

The blue-colored rays correspond to the blue equation above, while the brown-colored ray is matched to the brown equation.

Four of the blue roots correspond to the original quadratic equation for $\sin x$. The second unique value of $\sin x$ from these roots is the second root of the quadratic equation, $(-\sqrt5+1)/4$, and it corresponds to $x=-\pi/10$. Thus we have retrieved $\sin^{-1}[(-1+\sqrt5)/4]=\pi/10$ along with $\sin^{-1}[(1+\sqrt5)/4]=3\pi/10$. Such a dual result would be expected from any method based on the quadratic equation.

We see that introducing the $\cos x$ factor completes a fivefold symmetric set of the blue roots. This offers a geometric/symmetry-related explanation why the $\cos x$ multiplier worked as well as it did. This multiplier also introduced a root not part of the symmetric group, which corresponds to the brown equation.

Answer 2

Let $\cos y = \frac{\sqrt5+1}4$. Then $$\cos 2y =2\cos^2 y-1= 2\left(\frac{\sqrt5+1}4\right)^2-1=\frac{\sqrt5-1}4$$ $$\cos 4y =2\cos^2 2y-1= -\frac{\sqrt5+1}4= -\cos y= \cos(\pi\pm y)$$ The $+$ sign leads to $y=\frac\pi3$ while the $-$ sign leads to $y=\frac\pi5$. But then the value above for $\cos 2y$ is positive so we must have $y<\frac\pi4$. Therefore, $y=\frac\pi5$ is selected and $x=\frac\pi2-\frac\pi5=\frac{3\pi}{10}$.

Answer 3

Hint for this particular problem. The fraction $$ \frac{1 + \sqrt{5}}{4} $$ is half the golden ratio $$ \varphi = \frac{1 + \sqrt{5}}{2} $$ which strongly suggests that a regular pentagon is involved. It's no surprise that the answer $3\pi/10$ has denominator divisible by $5$.

You can work out by inscribing this pentagon picture from cut-the-knot in a unit circle: 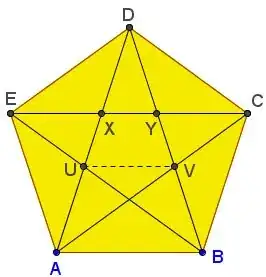in which $$ \frac{DE}{EX} = \frac{EX}{XY} = \frac{UV}{XY} = \frac{EY}{EX} = \frac{BE}{AE} = \varphi $$