How to find a point on an ellipse whose normal intersects a point outside the ellipse?

Question

I'm not a math person or coder, so please be patient with me. If I have an ellipse using this equation: $$\frac{(x-h)^2}{a^2}+\frac{\left(y-k\right)^2}{b^2}=1$$

And I know the values $a,b,h,k,x',y'$ how do I calculate the coordinates for a point on the ellipse where the normal intersects $x',y'$?

I did find this solution here: How to find the point on an ellipse that is closest to the point A outside of the ellipse

But I don't understand how to use the equations, and also can't comment to ask for help because I don't have enough reputation points.

Much appreciated!

Answer 1

A central conic has at most $4$ concurrent normals from a given point.

Given an ellipse

$$\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1 \tag{1}$$

The equation of the normal at $(X,Y)$ is

$$\frac{(X-h)(y-Y)}{a^2}-\frac{(x-X)(Y-k)}{b^2}=0$$

If $B$, $C$, $D$ and $E$ are the feet (or pedals) of the concurrent normals from $A(x',y')$, then switching the roles of $(x,y)$ and $(X,Y)$ gives an Apollonian rectangular hyperbola

$$\frac{(x-h)(y-y')}{a^2}-\frac{(x'-x)(y-k)}{b^2}=0 \tag{2}$$

on which $A$, $B$, $C$, $D$ and $E$ are lying. Hence, the intersections of $(1)$ and $(2)$ are the required feet of the concurrent normals.

• There will be $4$ concurrent normals when

$$[a(x'-h)]^{2/3}+[b(y'-k)]^{2/3}<(a^2-b^2)^{2/3}$$

• There will be $3$ concurrent normals when

$$[a(x'-h)]^{2/3}+[b(y'-k)]^{2/3}=(a^2-b^2)^{2/3}$$

that is $A$ lies on the ellipse evolute.

• There will be $2$ concurrent normals when

$$[a(x'-h)]^{2/3}+[b(y'-k)]^{2/3}>(a^2-b^2)^{2/3}$$

• For $a^2>2b^2$, part of the evolute will be outside the ellipse. There'll be two to four normals concurrent at $(x',y')$. The problem can be solved graphically by finding the intersections of the two conics. The pictures are generated by Geogebra.

See my derivation for an oblique case of central conics here and also the case of hyperbola for your further interest.

Answer 2

Assuming that you want $(x',y')$ to be on the normal ray exterior to the ellipse, as shown in your diagram, your question is indeed looking for the point $(x,y)$ on the ellipse closest to $(x',y')$. There could be as many as three other points from which a line normal to the ellipse intersects $(x',y')$, but I believe in all those cases the line will have to pass through the ellipse between $(x,y)$ and $(x',y')$.

For application to a software program, I think you're going to want to use a numerical root-finding function.

The coordinates of any point $(x,y)$ on the ellipse can be parameterized by $$ \begin{align} x &= h + a\cos\theta, \\ y &= k + b\sin\theta, \end{align} \tag1 $$ where you can let $\theta$ range from $0$ to $2\pi$ if you want to cover every point on the ellipse. The distance from $(x,y)$ to $(x',y')$ as a function of $\theta$ is then $$ d(\theta) = \sqrt{(x' - h - a\cos\theta)^2 + (y' - k - b\sin\theta)^2}. $$

So that's the function whose value you want to minimize. Since the minimum value of $d(\theta)$ will coincide with the minimum value of $(d(\theta))^2$, you can also solve this by minimizing $$ f(\theta) = {(x' - h - a\cos\theta)^2 + (y' - k - b\sin\theta)^2}. $$

You can restrict the possible values of $\theta$ depending on the location of $(x',y')$ relative to $(h,k)$, for example, if $x'>h$ and $y'>k$ then $(x',y')$ is in the first quadrant relative to the ellipse and therefore you only need to consider $0 < \theta < \frac\pi2.$ Once you have made such a restriction, any point at which $f'(\theta) = 0$ will be a point at minimum distance from $(x',y')$, because there are no inflection points in $f(\theta)$ and the restriction on $\theta$ rules out any maximum inside the interval. Now, $$ f'(\theta) = 2a(x' - h - a\cos\theta)\sin\theta - 2b(y' - k - b\sin\theta)\cos\theta. $$

So you just need to find $\theta$ such that $$ a(x' - h - a\cos\theta)\sin\theta - b(y' - k - b\sin\theta)\cos\theta = 0. $$ This is where a numerical root-finding function comes in handy. If you cannot find one in any available math library for your script, one possibility is to implement the bisection method, which is not the most efficient method but is relatively simple to implement.

Once you find $\theta$ that minimizes $f(\theta),$ simply plug that value into Equation $(1)$ to get the desired values of $x$ and $y$.

Answer 3

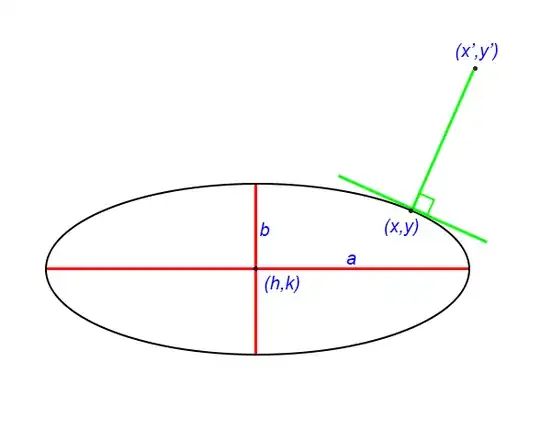
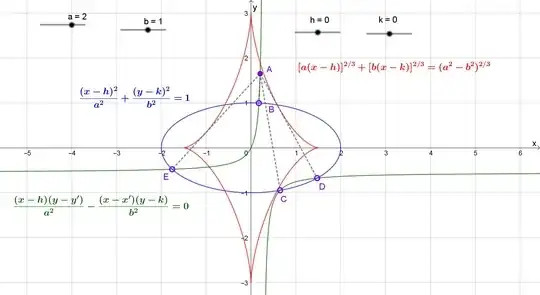
The parametric equations for the ellipse

$$ \dfrac{ (x - h)^2}{a^2} + \dfrac{ (y - k)^2}{b^2} = 1 $$

are:

$ x = h + a \cos t $

$ y = k + b \sin t $

The tangent vector is $( - a \sin t, b \cos t ) $, therefore the normal vector is

$ (b \cos t , a \sin t ) $

Hence we want to find $s$ such that

$ (h + a \cos t , k + b \sin t ) + s (b \cos t, a \sin t ) = (x', y') $

It follows that $s$ is given by

$ s = \dfrac{ x' - h - a \cos t }{ b \cos t } = \dfrac{ y' - k - b \sin t }{a \sin t } $

Cross multiplying, gives us,

$ a \sin t ( x' - h - a \cos t ) - b \cos t ( y' - k - b \sin t ) = 0 $

This equation is of the form

$ A \cos t + B \sin t + C \cos(2 t) + D \sin(2 t) + E = 0 $

where

$A = - b (y' - k)$

$B = a (x' - h) $

$ C = 0 $

$ D = \dfrac{1}{2} ( - a^2 + b^2 ) $

$ E = 0 $

The standard way to solve this equation it to introduce the transformation $ z = \tan \dfrac{t}{2} $, then it follows that

$ \cos t = 2 \cos^2 \dfrac{t}{2} - 1 = \dfrac{2}{z^2 + 1} - 1 = \dfrac{1 - z^2 }{1 + z^2} $

And similarly,

$ \sin t = 2 \cos \dfrac{t}{2} \sin \dfrac{t}{2} = 2 \cos^2 \dfrac{t}{2} \tan \dfrac{t}{2} = \dfrac{2z}{z^2 + 1} $

Using the above, we can find expressions for $\sin(2 t)$ and $\cos(2 t)$, namely

$ \sin(2 t) = 2 \sin t \ \cos t = \dfrac{ 4 z (1- z^2) }{(1 + z^2)^2} $

and

$ \cos(2 t) = 2 \cos^2 t - 1 = 2 \left( \dfrac{1 - z^2}{1 + z^2} \right)^2 - 1 = \dfrac{z^4 - 6 z^2 + 1 }{(1 + z^2)^2} $

Substituting these expressions in to the equation and multiplying through by $(1 + z^2)^2 $ results in a quartic (degree $4$) polynomial in $z$, which can be solved using the quartic polynomial roots formula, or numerically. Once the $z$-roots are found, the angle $t$ corresponding to each root $z$ is computed as $ t = 2 \tan^{-1} z $.