6

I am working on a project where I need a formula to find the point $B(x,y)$ on the ellipse $x^2+4y^2=r^2$ that is closest to the point $A(x_0,y_0)$, where $A$ is known and is outside the ellipse.

I have been trying to use the distance formula $d=\sqrt{(x-x_0)^2+(y-y_0)^2}$ but I have been running into some problems trying differentiate.

Any help would be greatly appreciated.

Intelligenti pauca
  • 55,765
andrewvb
  • 63
  • 3
    You could always try the trick of squaring the distance and minimizing that. Your derivatives will likely be much simpler. – Adrian Keister May 17 '18 at 14:48
  • 1
    There can be up to four points where the derivative of $d$ vanishes, hence the equation you get from $d'=0$ is in general a quartic. – Intelligenti pauca May 17 '18 at 15:24
  • 1
    @AdrianKeister: no, this doesn't simplify the problem at all, believe me. –  May 19 '18 at 16:48

2 Answers2

3

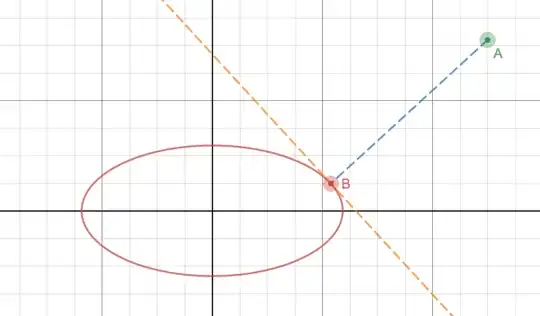
enter image description here (see Desmos implementation here.)

New Answer

Point on Ellipse: $$B(x,y)=(r\cos\theta, \frac r2\sin\theta)\\ B'(x', y')=(-r\sin\theta, \frac r2 \cos\theta)\\$$

When $B$ is the nearest point to $A$, $$\begin{align} (\mathbf b-\mathbf a)\cdot \mathbf b' &=0\\ \left(\begin{array}.r\cos\theta-x_0\\\frac r2\sin\theta-y_0\end{array}\right) \cdot \left(-r\sin\theta\atop \frac r2\cos\theta\right) &=0\\ (r\cos\theta-x_0)(-r\sin\theta)+(\tfrac r2\sin\theta-y_0)(\tfrac r2\cos\theta) &=0\\ -2r\sin\theta+2x_0\tan\theta+\frac r2\sin\theta-y_0&=0\\ \tfrac 32 r \sin\theta-2x_0\tan\theta+y_0&=0 \end{align}$$

Solving for $\theta$ gives coordinates for $B$.

Previous Answer

Point on Ellipse: $$B(x,y)=(r\cos\theta, \frac r2\sin\theta)\\ B'(x', y')=(-r\sin\theta, \frac r2 \cos\theta)\\ \frac {dy}{dy}=-\frac 1{2\tan\theta}=m_1\qquad \text{(slope at $B$)}$$ Slope of $AP$: $$m_2=\frac {y-\frac r2\sin\theta}{x_0-r\cos\theta}$$ $B$ is the nearest point on the ellipse to $A$ when $AB$ is perpendicular to the tangent at $B$, i.e.

$$m_1m_2=-1\\ -\frac 1{2\tan\theta}\cdot\frac {y-\frac r2\sin\theta}{x_0-r\cos\theta}=-1\\ 2x_0\tan\theta-\frac 32r\sin\theta=y_0$$ Solving for $\theta$ gives the coordinates for $B$.

Hypergeometricx
  • 23,235
1

Not sure if efficient, but here is how I would do it:

Rewrite the ellipse as a function: $$f_{1,2}(x):=\pm\frac{1}{2} \sqrt{r^2-x^2}$$

Using the distance formula, we get the following functions: $$d_{1,2}(x):=\sqrt{(f_{1,2}(x)-y_0)^2+(x-x_0)^2}$$

Now we minimize $d_{1,2}(x)$ by solving ${d_{1,2}}'(x)=0$:

Suppose $A$ is $(1,1)$ and $r=1$, so we use $f_1(x)$: $$d_1(x)=\sqrt{\left(\frac{\sqrt{1-x^2}}{2}-1\right)^2+(x-1)^2}\\d_1'(x)=\frac{x \left(\frac{1}{\sqrt{1-x^2}}+\frac{3}{2}\right)-2}{\sqrt{3 x^2-4 \sqrt{1-x^2}-8 x+9}}=0\tag{1}$$

Which gives one solution: $$\{\{x\to 0.69282\}\}$$

Plug this in $f_1(x)$ and we get $B(x,y)$ as: $$B(x,y)=\{0.69282,0.360555\}$$

If you have trouble solving for $x$ in$(1)$, you can always use numerical methods like Newton-Raphson.

John Glenn
  • 2,363
  • 12
  • 26
  • 1
    That definitely solves the problem, but I realize now that the question I should have asked is if there is a line between the origin of the ellipse and the point $A(x,y)$, where on the ellipse will it intersect. I will have to look that up now thanks for the help anyway. – andrewvb May 17 '18 at 15:51
  • 1
    That should be fairly easy, just write the equation of the line, and solve simultaneously the equation for the ellipse and the line. You should get two intersection points, but only one should be meaningful/relevant (the point between the origin and $A$) – John Glenn May 17 '18 at 15:59
  • Thanks, I was able to find the formulas for x and y for $B$. Here they are if anyone else is interested. $B_x =(A_xr)/sqrt{(A_x^2+4A_y^2)}$ and $B_y =(A_yr)/sqrt{(A_x^2+4A_y^2)}$ – andrewvb May 17 '18 at 16:34
  • @andrewvb - are you sure that's correct? – Hypergeometricx May 17 '18 at 17:24