Let
- $T>0$
- $I:=(0,T]$
- $X:\overline I\to\mathbb R$ be continuous with $X(0)=0$
- $\varepsilon>0$
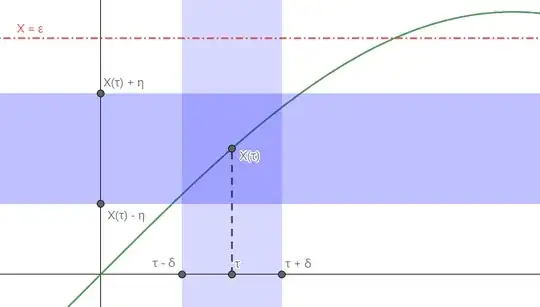
- $\tau:=\inf\left\{t\in\overline I:|X(t)|\ge\varepsilon\right\}$
- $t\in\overline I$
How can we show that $\tau\le t$ if and only if $|X(s)|\ge\varepsilon$ for some $s\in[0,t]$?
Clearly, the "if" part is trivial. However, I don't know how we need to argue in the "only if" part. For example, why isn't it possible that $\tau=t$, $|X(s)|<\varepsilon$ for all $s\in[0,t]$ and $|X(s)|\ge\varepsilon$ for all $s\in(t,T]$?