The Plane: $x+y=4$
The Cylinder: $y^2+9z^2=16$
I have gone this far but I'm not sure it's true $$V=\int\limits_0^4\int\limits_0^{4-x}\int\limits_0^{\sqrt{16-y^2}/9} dz\ dy\ dx$$ PS: Answer can contain $\pi$ if needed.
Asked
Active
Viewed 4,119 times
0
GNUSupporter 8964民主女神 地下教會
- 17,998
Deniz da King
- 133
- 2
- 5
2 Answers
1
\begin{align} V&=\int_0^4\int_0^{4-x}\int_0^{\sqrt{16-y^2}/3} dzdydx \\ &= \int_0^4\int_0^{4-y}\int_0^{\sqrt{16-y^2}/3} dzdxdy \\ &= \int_0^4 (4-y) \, \frac{\sqrt{16-y^2}}3 dy \\ &= \frac13 \left[ 4\int_0^4 \sqrt{16-y^2} dy - \int_0^4 y\sqrt{16-y^2} dy \right] \\ &= \frac13 \left[ 4 \, \frac{\pi(4^2)}{4} + \frac12 \int_0^4 \sqrt{16-y^2} d(16-y^2) \right] \\ &= \frac13 \left[ 4 \, \frac{\pi(4^2)}{4} - \frac12 \,\frac23 \, 16^{3/2} \right] \\ &= \frac13 \left( 16\pi - \frac{64}{3} \right) \\ &= \frac{16(3\pi-4)}{9} \end{align}
Comparison of my answer with another answer
Since pictures are used for illustration, let me also use them.
- Another answer: fix $x$ first. This gives rise to a more complicated integrand
$$V = \frac13\int_0^4 \int_0^{4-x} \sqrt{16-y^2} dydx$$
As the shaded area of the graph illustrates, one needs to sum the area of a triangle and the sector (involving inverse trigonometric function). That's why wolfram-alpha complains "standard computation time exceeded...".
- My answer: fix $y$ first. This change of order of integration kills two inner integrals, leaving a much simpler integrand in $y$ only. This allows wolfram-alpha to give the exact solution.
GNUSupporter 8964民主女神 地下教會
- 17,998
-
-
@gimusi Thanks, fixed. You're right b/c $$y^2+9z^2=16 \iff z^2 = \frac{16-y^2}{9}.$$ You may compare your approach (fix $x$ first) with mine (fix $y$ first). Both yields an approximate solution $9.64405$ on Wolfram Alpha, but your approach doesn't give the exact form in the standard computation time. – GNUSupporter 8964民主女神 地下教會 May 12 '18 at 17:12
-
@gimusi Thanks for the answer. I'm glad that I almost set up the integral correctly. Looks like I only forgot how to integrate $\sqrt{16-y^2}$ Can you explain me what exactly you did to integrate that? – Deniz da King May 12 '18 at 18:42
-
@DenizdaKing I don't do a $u$-substitution to integrate this. Sometimes, thinking of the geometric meaning of questions can lead to unexpectedly elementary but elegant solutions. – GNUSupporter 8964民主女神 地下教會 May 12 '18 at 18:48
-
@DenizdaKing Your set up is uncorrect, indeed you need to fix $\sqrt{\frac{16-y^2}{9}}$ for the integral refer to https://math.stackexchange.com/q/533082/505767 – user May 12 '18 at 18:50
0
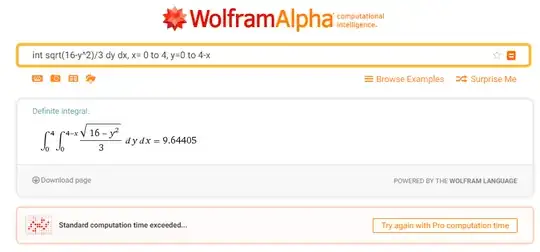
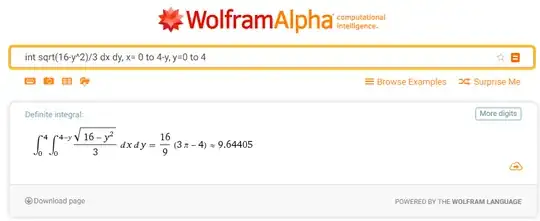
Yes it is (almost) correct, indeed we need to consider that the plane intersect the cylinder according to the following sketch, then the set up is as follow
$$V=\int_0^4 dx\int_0^{4-x}dy\int_0^{\sqrt{\frac{16-y^2}{9}}} dz$$
user
- 162,563
\fracin exponents or limits of integrals. – GNUSupporter 8964民主女神 地下教會 May 12 '18 at 17:32