2

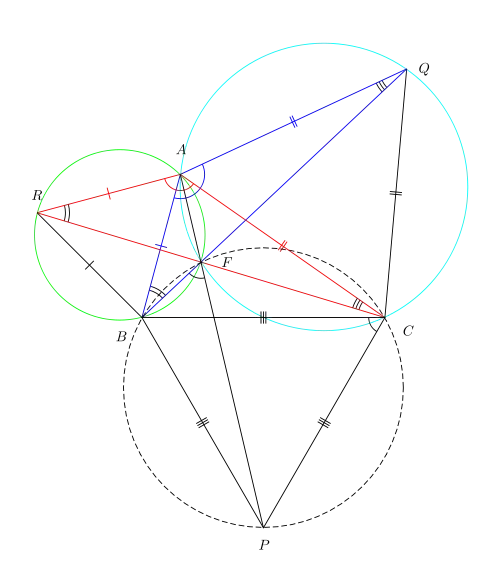
If $x,y,z$ are real and positive and they verify the system $$\begin{cases} x^2+xy+y^2=36\\ y^2+yz+z^2=64\\ z^2+zx+x^2=100 \end{cases}$$ Find the value of the sum $S=xy+yz+zx$

Of course I tried the obvious, to sum them all up, to bring each equation to the canonical form, to guess. I can see that the system is symmetric, but I don't know how does it help. Someone who already solved it told me that $S$ is proportional to $\sqrt{3}$. How to proceed?

asd11
  • 508

2 Answers2

4

(Solution edited to give a value of $S$.)

  1. By the Cosine Law of , $x^2+y^2-2xy(\cos 120°) = 6^2$, so an obtuse triangle of side lengths $x,y,6$ with internal angle $120°$ facing the longest side with length $6$ is formed. Idem for the other two inequalities.
  2. Observe that a triangle with lengths $6$-$8$-$10$ is a right-angled triangle. (Denoted $\triangle ABC$.)
    enter image description here
    For each of the given equation, one of the smaller arcs $\newcommand{arc}[1]{\stackrel{\Large\frown}{#1}} \arc{AB},\arc{BC},\arc{CA}$ represents the locus of the vertex with the largest angle of the corresponding obtuse triangle.
  3. It's well known in that these three arcs coïncide at the Fermat point $F$ of $\triangle ABC$. Since $\triangle ABC$ contains no internal angle larger than $120°$, $F$ lies inside $\triangle ABC$.
  4. No need to solve for the variables $x,y,z$. (represented by $AF, BF, CF$) Use a property of the Fermat point that the angles formed by $AF, BF, CF$ are $120°$. \begin{align} \text{Area of } \triangle ABC &= \text{Area of } \triangle ABF + \text{Area of } \triangle BCF + \text{Area of } \triangle ACF \\ \frac{6 \times 8}{2} &= \frac12 xy (\sin 120°) + \frac12 yz (\sin 120°) + \frac12 zx (\sin 120°) \\ 24 &= \frac{\sqrt3}{4} (xy+yz+zx) \\ S &= 32 \sqrt 3 \end{align}
GNUSupporter 8964民主女神 地下教會
  • 17,998
  • Quite impressive. Thank you! I was looking though for sth more algebraic! – asd11 May 12 '18 at 08:15
  • @asd11 Thanks for upvote and comment. I understand this. However, if you're lucky enough, a geometrical solution can be are more elegant and elementary than an analytical one (using algebra and/or multivariable calculus), so as minimizing the sum of distances of some geometrical figure. – GNUSupporter 8964民主女神 地下教會 May 12 '18 at 08:41
  • Would you mind it to share which software you used to draw that beautiful image? Thanks in advance. – XavierStuvw Nov 23 '21 at 09:27
  • 1
    @XavierStuvw Sorry for my late response. I used a relevant image from Wiki to save time. In the picture $\triangle ABC$ isn't a right-angled, but it should be from my answer. I believe that the author of this good-looking picture used TikZ, which is quite time-consuming to learn, but the resulting images would look impressive. I'm taking an indefinite break from this site to learn more SVG. – GNUSupporter 8964民主女神 地下教會 Mar 22 '22 at 11:28
3

If you are willing to use Wolfram Mathematica then the answer comes out as

In[1]:= (x y+y z+z x)^2 /. Solve[{x^2+x y+y^2 == 36,
     y^2+y z+z^2 == 64, z^2+z x+x^2 == 100}] //
     Simplify //Sqrt //InputForm
Out[1]//InputForm=
     32*Sqrt[3], 32*Sqrt[3], 32*Sqrt[3], 32*Sqrt[3]}

and so the answer is $\;32\sqrt{3}.$

Alternatively, define

$$ q_1 := x^2+xy+y^2,\; q_2 := y^2+yz+z^2,\; q_3 := z^2+zx+x^2 $$

and also let

$$ e_1 := x+y+z,\; e_2 := xy+yz+zx,\; e_3 := xyz. $$ Given that $\;q_1=36, q_2=64, q_3=100,\;$ then $\;q_1+q_2+q_3 = 2e_1^2-3e_2 = 200\;$ and $\;q_1q_2+q_2q_3+q_3q_1 = e_1^4 + 3e_2^2 -3e_2e_1^2 = 12304.\;$ Now from the first equation $\;e_2=(2e_1^2-200)/3\;$ and when substituted into the second equation gives $\;(40000-200e_1^2+e_1^4)/3 = 12304\;$ with solution $\;e_1^2 = 100+48\sqrt{3},\;$ and now $\;e_2 = 32\sqrt{3}.$

Somos
  • 37,457
  • 3
  • 35
  • 85