Find the altitude of a tetrahedron whose faces are congruent triangles

Question

Any set of four identical triangles can be arranged to form a four-surface solid. If these four triangles are not equilateral, e.g. 3,4,5, how do I find the altitude of from the one used for the bottom to the apex formed by the other three.

Answer 1

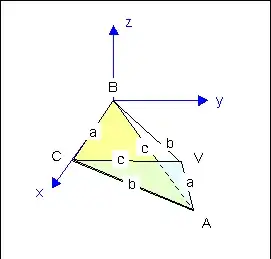
Since Tetrahedron is usually meant to designate the regular polyhedron, we can better say that we are constructing a triangular Pyramid.

Intuitively speaking, we are starting with two identical sets of three "poles", having different lengths but respecting the triangular law.

With one set we construct the base, $\triangle{ABC}$, and we designate, as usual, with $a$ the length of the edge opposed to $A$, with $\alpha$ the angle in $A$, etc.

Thereafter, with the second set of poles we are going to construct a "tent" over the base.
To do that, we order the poles in a non-decreasing order, e.g. $a,b,c$.
We place the shortest $a$ in $A$, the longest $c$ in $C$, and $b$ in $B$, and join at the top $V$.
We have obtained four exact copies of the triangle $ABC$, arranged congruently.
And there is no other way to arrange them.
The sum of the angles in $V$ is $\pi < 2\pi$, so everything looks to be in place.

Now we place a reference system with the origin in one vertex, and one edge of the base along the $x$ axis, as in the sketch.
To obtain the position of $V$, we impose to the vector $\bf b = \vec{BV}$ to make an angle $\gamma$ with $\bf a = \vec{BC}$ and an angle $\alpha$ with $\bf c = \vec{BA}$, and to have a length of $b$.
That means $$ \left\{ \matrix{ \left( {\matrix{ a & 0 & 0 \cr {c\cos \beta } & {c\sin \beta } & 0 \cr } } \right) \left( {\matrix{ {v_x } \cr {v_y } \cr {v_z } \cr } } \right) = \left( {\matrix{ {ab\cos \gamma } \cr {cb\cos \alpha } \cr } } \right) \hfill \cr \left( {\matrix{ {v_x } & {v_y } & {v_z } \cr } } \right) \left( {\matrix{ {v_x } \cr {v_y } \cr {v_z } \cr } } \right) = b^{\,2} \hfill \cr} \right. $$ which is readily solved as $$ \bbox[lightyellow] { \left\{ \matrix{ v_x = b\cos \gamma \hfill \cr v_y = b\left( {\cos \alpha - \cos \beta \cos \gamma } \right)/\sin \beta \hfill \cr v_z = b\sqrt {1 - \cos ^{\,2} \gamma - \left( {\cos \alpha - \cos \beta \cos \gamma } \right)^{\,2} /\sin ^{\,2} \beta } \hfill \cr} \right. }\tag{1}$$

$v_z$ is the heigth to compute the volume, which thus will be $$ \bbox[lightyellow] { \eqalign{ & V = {1 \over 6}abc\sqrt {\left( {1 - \cos ^{\,2} \gamma } \right)\sin ^{\,2} \beta - \left( {\cos \alpha - \cos \beta \cos \gamma } \right)^{\,2} } = \cr & = {1 \over 6}abc\sqrt {1 + 2\cos \alpha \cos \beta \cos \gamma - \left( {\cos ^{\,2} \gamma + \cos ^{\,2} \beta + \cos ^{\,2} \alpha } \right)} \cr} }\tag{2}$$ which can be then reformulated in various ways by using the sine or cosine laws.

But .., whoever has practically built any such a tent, or origami, or else, might smell that it can't go always so .. straight.
And in fact, if one of the angles, e.g. $\gamma$, is rect, in the above we get $v_x=0$.
Some investigation shows that the tent has become flat, with $AVBC$ that becomes a rectangle.
And some more investigation shows that the construction (always dealing with four equal triangles) is:
- possible when all the angles are less than $\pi/2$ (acute triangles),
- becomes flat if one angle is $\pi/2$,
- and is impossible if the triangles are obtuse.

Note that, by replacing $\alpha$ with $\pi - \alpha -\beta$ and then putting it back, we can rewrite the result above as

$$ \bbox[lightyellow] { \eqalign{ & V^{\,2} = {1 \over {36}}a^{\,2} b^{\,2} c^{\,2} \left( {\left( {1 - \cos ^{\,2} \gamma } \right)\sin ^{\,2} \beta - \left( {\cos \alpha - \cos \beta \cos \gamma } \right)^{\,2} } \right) = \cr & = {1 \over {36}}a^{\,2} b^{\,2} c^{\,2} \left( {\sin ^{\,2} \gamma \sin ^{\,2} \beta - \left( {\cos \left( {\pi - \left( {\beta + \gamma } \right)} \right) - \cos \beta \cos \gamma } \right)^{\,2} } \right) = \cr & = {1 \over {36}}a^{\,2} b^{\,2} c^{\,2} \left( {\sin ^{\,2} \gamma \sin ^{\,2} \beta - \left( {2\cos \beta \cos \gamma - \sin \beta \sin \gamma } \right)^{\,2} } \right) = \cr & = {1 \over {36}}a^{\,2} b^{\,2} c^{\,2} \left( { - 4\cos ^{\,2} \beta \cos ^{\,2} \gamma + 4\cos \beta \cos \gamma \sin \beta \sin \gamma } \right) = \cr & = {1 \over 9}a^{\,2} b^{\,2} c^{\,2} \cos \alpha \cos \beta \cos \gamma \cr} }\tag{2.a}$$ which coincides with the more mathematically elegant method provided by Blue.
And we can rewrite more compactly also the (1).

Answer 2

Elaborating on my comment ...

Let the triangle have side-lengths $a$, $b$, $c$, and area $T$. The Cayley-Menger determinant for area ---equivalently Heron's formula--- tells us $$16 T^2 = (-a+b+c)(a-b+c)(a+b-c)(a+b+c) \tag{1}$$ The CM determinant for volume gives $$288V^2 = \left|\begin{matrix} 0 & 1 & 1 & 1 & 1 \\ 1 & 0 & a^2 & b^2 & c^2 \\ 1 & a^2 & 0 & c^2 & b^2 \\ 1 & b^2 & c^2 & 0 & a^2 \\ 1 & c^2 & b^2 & a^2 & 0 \end{matrix}\right| = 4 (-a^2 + b^2 + c^2) (a^2 - b^2 + c^2) (a^2 + b^2 - c^2) \tag{2}$$

Observe that, if the triangle has a right angle, then $(2)$ vanishes; the tetrahedron has zero volume. Moreover, if the triangle has an obtuse angle, then $(2)$ is negative, making $V$ imaginary: in this case, there must be no tetrahedron at all.

Since altitude $h$ satisfies $3 V = h T$,

$$h^2 = \frac{9 V^2}{T^2} = \frac{2(-a^2+b^2+c^2)(a^2-b^2+c^2)(a^2+b^2-c^2)}{(-a+b+c)(a-b+c)(a+b-c)(a+b+c)} \tag{$\star$}$$

For something more angle-related ... By the Law of Cosines, we have $$a^2 = b^2 + c^2 - 2 b c \cos A \qquad\text{etc}$$ so that $$V^2 = \frac{1}{72}\cdot 2 b c \cos A \cdot 2c a \cos B \cdot 2 a b \cos C = \frac{1}{9} a^2 b^2 c^2 \cos A \cos B \cos C$$ By the Law of Sines, $$a = d \sin A \qquad\text{etc}$$ where $d$ is the circumdiameter of the triangle, so that $$T = \frac12 a b \sin C = \frac12 d^2 \sin A \sin B \sin C \qquad V = \frac13 d^3\sin A \sin B \sin C\sqrt{\cos A \cos B \cos C} $$ Hence,

$$h = \frac{3V}{T} = 2d\sqrt{\cos A \cos B \cos C} \tag{$\star\star$}$$

Answer 3

You have 3 legs for 1 triangle and it is repeated to make 4 triangles, which fit together to make some wierd tetrahedron. Therefore, we are given 3 of 4 total points. Assume them to be $(A_x,A_y,A_z),(B_x,B_y,B_z),(C_x,C_y,C_z)$. Once fitted, the fourth point, $D(x,y,z)$, can be found by some combination for a solution to the following three equations. $$\Vert (x,y,z)-A)\Vert = \Vert(B-A)\Vert$$ $$\Vert (x,y,z)-B\Vert = \Vert(C-A)\Vert$$ $$\Vert(x,y,z)-C\Vert=\Vert(B-C)\Vert$$ Using real 3d points for A,B,C Geogebra easily comes up with the two options for point $D$. From here it is just more analytic geometry. We are looking for the distance from the new point, $D$, to the plane made by points $A,B,C$.

The plane equations normal vector $(n_x,n_y,n_z)$ is given by getting the cross product of two vectors that are in the plane. The plane is then $$\left(\begin{array}{c}x\\y\\z\end{array}\right)\cdot\left(\begin{array}{c}n_{x}\\n_{y}\\n_{z}\end{array}\right)=\left(\begin{array}{c}A_{x}\\A_{y}\\A_{z}\end{array}\right)\cdot\left(\begin{array}{c}n_{x}\\n_{y}\\n_{z}\end{array}\right).$$ A line from point $D$ to the plane can be written as $$\left(\begin{array}{c}x\\y\\z\end{array}\right)=D+\lambda\left(\begin{array}{c}n_{x}\\n_{y}\\n_{x}\end{array}\right)$$

From here you can plug in $D$ and $n$ and get values for $(x,y,z)$ in terms of $\lambda$. i.e. little equations. Substitute these into the plane equation and solve for $\lambda$. Finally, plug lambda back into the line equation to get the intersection of the plane and the line, call it point $E$. $Distance = |D-E|$. It is a lot easier with numbers and probably easier to understand as well.

Answer 4

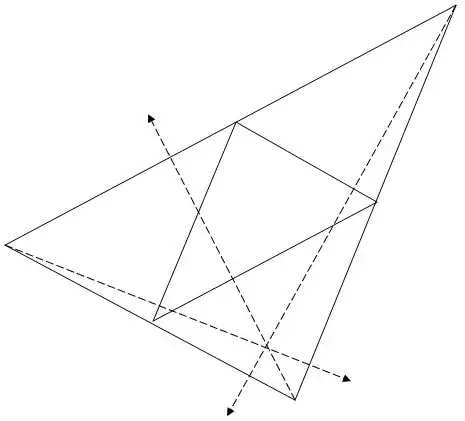
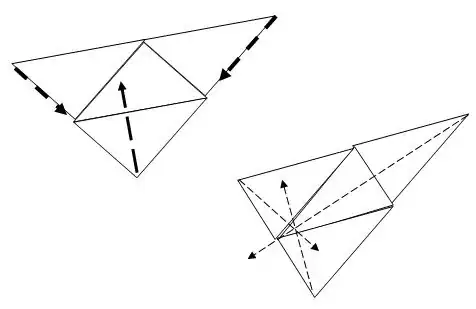
I had previously brought up the fact that I thought 4 identical triangles needed to be isosceles triangles to make a tetrahedron. I've added this sketch to show how isosceles triangles fold up to make a tetrahedron with the 3 apexes intersecting at a single point when folded up. Conversely, with a 3,4,5 triangle, when folded up, the apexes do not translate to a single point. Or am I missing something? Update, per the additional graphic, I guess it only works for acute triangles.

Answer 5

For 4 identical isosceles triangles, the height will be:

$$h = \sqrt{(b\cdot cos(A/2))^2-(b\cdot sin(A/2)tan(A/2))^2}$$

Where b is the base length, and A is the apex angle of the isosceles triangle.

Example: for 4 isosceles triangles with base 5 and apex angle 40 deg.....

$h = 4.657$