6

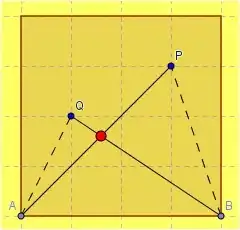
P and Q are uniformly distributed in a square of side AB. What is the probability that segments AP and BQ intersect?

enter image description here

nrb
  • 149

3 Answers3

11

Inspired by Lee David Chung Lin's answer.

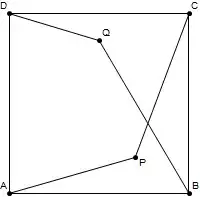
Consider the four events $$AP \cap BQ \neq \varnothing, \\ AP \cap DQ \neq \varnothing, \\ CP \cap BQ \neq \varnothing, \\ CP \cap DQ \neq \varnothing.$$

Ignoring degenerate configurations, the events are mutually disjoint, equiprobable, and cover the whole space. $p = 1/4$.

Maxim
  • 11,274
  • 1
    This is really great. The reason I felt it was necessary to awkwardly make rigorous the $1/4$ (argument in the last part of my post), was exactly due to the lack of symmetry on the $AB$-and-$PQ$ configuration with respect to the square. I think this is THE canonical treatment of it as a geometric probability problem. – Lee David Chung Lin May 02 '18 at 08:14
10

Suppose we start with $Q = (x, y)$. The admissible positions for $P$ will be in the triangle $BQR$ if $y < x$ or in the quadrilateral $BQRC$ if $y > x$. The areas are calculated from the sides and the heights, and $$p = \int_0^1 \int_0^x \frac {y (1 - x)} {2 x} dy dx + \int_0^1 \int_x^1 \left( 1 - \frac x {2 y} - \frac y 2 \right) dy dx = \frac 1 4.$$

Maxim
  • 11,274
7

Here's a "calculation free" cut-and-paste argument. Maybe one can try to skip the description and directly examine the figures too see how this serve as a proof-without-words.

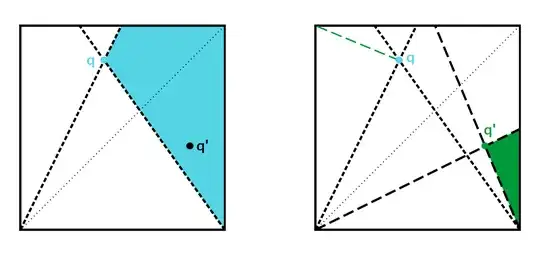
Consider point $Q$ confined to a quarter of the square $\square ABCD$, as shown in the left plot below. The plot on the right shows point $Q'$ as the reflection WRT (with respect to) the main diagonal $\overline{AC}$, point $q$ is reflected WRT the off-diagonal $\overline{BD}$, and point $q'$ is doubly-reflected (equivalent to rotating $Q$ WRT center of square by $180^{\circ}$). 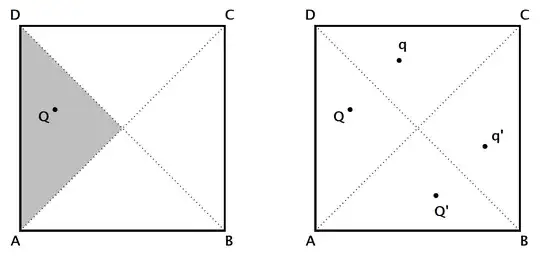First we consider the "admissible region" (this term borrowed from @Maxim) of $P$ that creates a crossing associated with $Q$, then we will combine the 4-fold symmetric mirror images associated with the full set $\{Q,Q',q,q'\}$.

The admissible region associated with $Q$ is highlighted below on the left (in magenta), and the region for $Q'$ is highlighted on the right plot (in blue). We can cut-and-paste the triangular blue "$Q'$ region" in the manner demonstrated below, thanks to the mirror symmetry by construct. The resultant quadrilateral consists of an obtuse triangle ($\triangle DQB$) plus THE isosceles right triangle, which is half of $\square ABCD$. 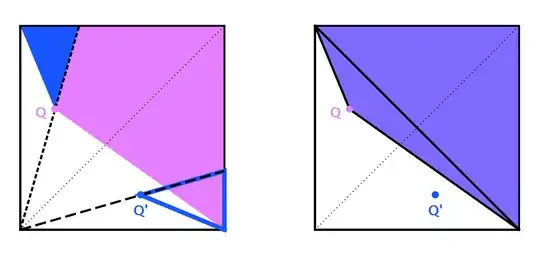Similarly, the admissible regions associated with $q$ and $q'$ can be cut-and-pasted into a quadrilateral that is half of $\square ABCD$ minus an obtuse triangle ($\triangle DqB$). 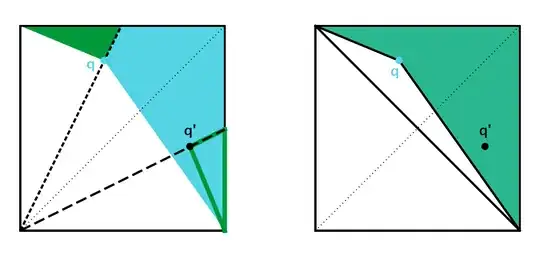Due to the symmetry WRT the off-diagonal, we can cut-and-paste (flip) the combined-$(q,q')$-region and have the exact full square. Since we effectively quadrupled the admissible region to arrive at unity, the actual probability is $1/4$.

Lee David Chung Lin
  • 7,297
  • 2
    A really nice answer. I suppose the last part can also be explained by saying that when computing the integral sums $S(x, y) \Delta x \Delta y$ over a symmetric grid, we can combine the four related terms, and the result will be the same as summing $\Delta x \Delta y / 4$. I've added another answer, exploiting the symmetry over the vertices of the square instead of the symmetries over the positions of $P$ and $Q$. – Maxim May 02 '18 at 08:03