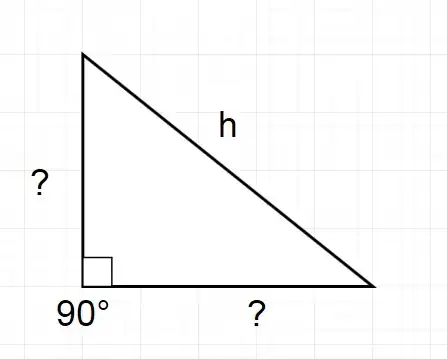8

Why the cosine of an angle of 90 degree is equal to zero?

By definition we know that: $$\text{cos } \alpha = \frac{\text{adjacent}}{\text{hypotenuse}}.$$

If we want to apply the definition to the situation in the image below:

enter image description here

we have that: $$\text{cos } 90° = \frac{?}{h} .$$ How can I say that it is equal to $0$ if I don't know anything about the other two sides, or about the other two angles?

I have been able to always find a value, even without the unit circle, in situations like $\text{csc } 90°, \text{sec } 0°$, etc..., But not in the above situation. Why?

Please, can you suggest me anything?

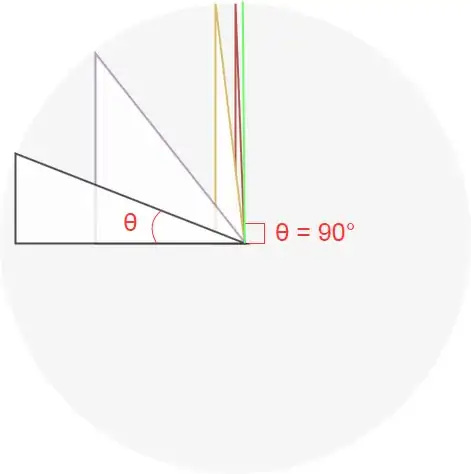
So, I make an addition also based on suggestions provided. My main error was to start to consider the right angle, instead I have to start considering $\theta = \alpha°$, and increse it till $\theta = 90°$, one side become smaller till zero, and the other side become bigger till equal to $h$, therefore $\text{cos } \alpha = \frac{0}{h} = 0$

enter image description here

JB-Franco
  • 862
  • Hint: the cosine in the rectangular triangle is defined as $\frac{adjacent}{hypotenuse}$ and you would have two angles of 90° in your triangle, making the third angle ... and thus the hypotenuse ... ? – R.J. Etienne Apr 22 '18 at 11:52
  • If your understanding of $\cos$ and $\sin$ comes only from right-angled triangles, then $\cos(90^\circ)$ makes no sense. You need to find some definition of the trigonometric functions which does not rely only on right-angled triangles (there are several conventional approaches, both geometric, algebraic and analytic, and most reasonable approaches give the same result in the end). Once you've done that you can again ask why $\cos(90^\circ)=0$. – Arthur Apr 22 '18 at 11:52
  • 2
    Hint: draw a triangle that has the angles $0,90^\mathrm{o},90^\mathrm{o}$ – MCCCS Apr 22 '18 at 11:54
  • It's a two-dimensional triangle. cool – Devin Peterson Oct 27 '22 at 04:03
  • Some have found the discussion in this ancient answer of mine helpful. – Blue Oct 24 '24 at 16:55

4 Answers4

5

Others have mentioned that such a right angle triangle does not exist.

As a compromise how about

$$\cos(45+45)=\cos(45)\cos(45)-\sin(45)\sin(45)=0 $$

The addition formula is easily justified geometrically.

I chose $45^{\circ}$ because you can work this exactly with an isosceles right angled triangle of side length $1,1,\sqrt{2}$

Karl
  • 4,763
2

While the trigonometric functions are initially defined for the angles of a triangle (in radians) they are extended to all real numbers, and eventually, to complex numbers. While their properties, such as the addition laws, are preserved, they eventually lose all connection with triangles.

In the case you give, it is clear that the adjacent side gets closer and closer to $0$ as the angle gets closer to $\pi/2$, so the cosine gets close to $0,$ but you obviously can't really have a triangle with two right angles.

saulspatz
  • 53,824
1

There is a flaw in your reasoning. When doing trigonometry (in a classical way) we consider a right angled triangle. The value of $\cos(\alpha)$ is commonly geven as the ratio $\frac{\text{adjacent side}}{\text{hypotenuse}}.$ This definition, however, is incomplete and would not be found like this in Dutch school books for instance. Dutch shool books would say something like: $$\cos (\alpha)=\frac{\text{aanliggende $\color{red}{\text{rechthoeks}}$zijde}}{\text{hypotenusa}}.$$ The important distinction here is that "rechthoekszijde" can't just be any side of a triangle. A "rechte hoek" is a right angle, and a "rechthoekszijde" is a side of a right angled triangle that is adjacent to its right angle (so not the hypotenuse by definition).

This means that if you want to deduce what $\cos(90^\circ)$ should be, you need to make sure that the adjacent side is not just adjacent to the angle $\alpha$, but also to the right angle of the triangle.

N.B. Keep in mind that this means that $\cos(90^\circ)$ can only be "observed" in a triangle with two right angles. You can interpret this in multiple ways: a degenerate triangle with one vertex at the point at infinity; the limit $\lim_{h\to\infty}\frac{\text{a}}{\text{h}}$; perhaps some other way.

In any case, the key point here is this:

When doing classical trigonometry, in normal case but definitely also in "extreme" cases, you need to define adjacent side and opposite side in such a way that either of them can never be the hypotenuse.

Below is a picture in which I try do demonstrate how you can use classical trigonomtry to define the trigonometric functions consistently outside $[0,\frac\pi2)$ = $[0^\circ,90^\circ)$.

Picture of right angled triangle with one acute angle very near 90 degrees

For instance, if the angle gets bigger than $90^\circ$ then $C$ will come to lie below $B$ in stead of above and we consider "opposite" and "hypotenuse" to be negative.

h4nek
  • 70
  • 5
gebruiker
  • 6,272
0

Because at $\cos(\pi/2)$ the hypotenuse is the y axis and the sin value itself.

There is no triangle, no theta exists there in the unit circle.

Just a straight line. $\sin x$ is the $y$ value itself and $\cos x$ is the x value itself.

That’s also why $\cos$ of zero is $1$ in the unit circle.

The sin of $\pi/2$, in the zero $x$ value position, is also one.

If that doesn't confuse out of you it does me.

$\sin$ of 90 degrees or $\pi/2$ is not the same as $\sin$ of zero which is zero.

Although it is in the zero $\cos$ or zero $x$ position on the unit circle.

clydekat21
  • 1