Given $$\sqrt{a +\sqrt{a-x}}+\sqrt{a-\sqrt{a+x}}=2x$$ and $a\in\Bbb{R}$, express $x$ in terms of $a$.
I rationalised the above expression and then again rationalised which gave me :
$$\sqrt{a+\sqrt{a-x}}-\sqrt{a-\sqrt{a+x}}=\frac{1}{\sqrt{a+x}-\sqrt{a-x}}$$
Now, what should I do?
If didn't rationalised the original Equation, or if the squared both sides twice then too bi-quadratic or higher degree polynomial will be obtained.
What should be done?
Here is a simplification, which leads to a parametrized solution.
Write the original equation as two equations
$$
\sqrt{a +\sqrt{a-x}} = x +q\\
\sqrt{a-\sqrt{a+x}}= x -q
$$
where $q$ is a function of $a$.
Double squaring both equations gives
$$
(x+q)^4-2a(x+q)^2+x+a^2-a = 0 \\
(x-q)^4-2a(x-q)^2-x+a^2-a = 0
$$
Subtracting and adding gives the two equations
$$
x^2+q^2-a -\frac{1}{4q}= 0 \\
x^4+ 6 q^2x^2 + q^4-2a(x^2+q^2)+a^2-a = 0
$$
The first equation gives the result
$$
x = \sqrt{-q^2+a +\frac{1}{4q}}= \sqrt{a + f(q)}
$$
with the offset $f(q)$. In here, $q$ has to be inserted, where $q = q(a)$ is obtained by replacing all terms with $x^2$ in the second equation with the first equation, giving
$$
(-q^2+a +\frac{1}{4q})^2+ 6 q^2(-q^2+a +\frac{1}{4q}) + q^4-2a(a +\frac{1}{4q})+a^2-a = 0
$$
Expanding this expression gives an implicit formula for $q(a)$ as follows:
$$
- 64 q^6 + 64 a q^4 + 16 q^3 - 16 a q^2 + 1 = 0
$$
I wasn't able to solve this further for $q$. However, the equations directly lead to a parametrized solution. Let $q$ be a free parameter. The range where $q$ is to be chosen from is discussed below. Then for each $q$, we have $a$ and $x$ according to
$$
a = \frac{64 q^6 - 16 q^3 - 1}{64 q^4 - 16 q^2} \\
x = \sqrt{-q^2+a +\frac{1}{4q}}
$$
The following observations can be made:
For large $a$, the equation for $a$ gives $q^2 \to \frac{1}{4}$. This can also be observed by regarding the very first set of two equations and treating $q$ as a small disturbance, which can in first order be neglected if all other terms grow exceedingly large. We then have $$ \sqrt{a +\sqrt{a-x_1}} = x_1\\ \sqrt{a-\sqrt{a+x_2}}= x_2 $$ which are solved (see Solve the equation: $x=\sqrt{a-\sqrt{a+x}},(a\geq 1)$) by $$ x_1 = \frac12 + \sqrt{a -3/4}\\ x_2 = -\frac12 + \sqrt{a -3/4} $$ So indeed, the $x_{1,2}$ grow exceedingly large, and $q = -\frac12$ gives both the correct offset term $-\frac34$ under the previous root $ x = \sqrt{-q^2+a +\frac{1}{4q}} $, as well as the two deviations $x - x_{1,2}$. For small $a$, correction terms must be added to $q(a)$ (in the sense of an expansion).
Addendum:
1. As a side observation, one can use the two solutions $x_{1,2}$ to establish that the modified equation
$$
\sqrt{a +\sqrt{a-x -\frac12}}+\sqrt{a-\sqrt{a+x-\frac12}}=2x
$$
is solved by $x = \sqrt{a -3/4}$.
$\color{brown}{\mathbf{\text{Reformulation of the problem.}}}$
At first, let us try to find any solution, using substitutions $$y=\sqrt{a+x},\quad z=\sqrt{a-x},\tag1$$ then $$x=y^2-a=a-z^2,\quad a \ge 0,\quad x\ge 0,\tag2$$ \begin{cases} \sqrt{a-y}+\sqrt{a+z} = y^2-z^2\\ y^2+z^2=2a\\ 0\le z\le \sqrt a \le y,\tag3 \end{cases} Let
$$u=\sqrt{a-y}=\sqrt{a-\sqrt{a+x}},\quad v=\sqrt{a+z} = \sqrt{a+\sqrt{a-x}},\tag4$$
then $$y=a-u^2,\quad z=v^2-a,\quad x=(a-u^2)^2-a=a-(v^2-a)^2,\tag5$$ \begin{cases} u+v=(a-u^2)^2-(v^2-a)^2\\ (a-u^2)^2+(v^2-a)^2=2a\\ 0\le v^2-a\le \sqrt a\le a-u^2\\ 0\le u\le \sqrt a\le v, \end{cases} or \begin{cases} u+v=(v^2-u^2)(2a-u^2-v^2)\\ u^4+v^4 -2a(u^2+v^2+1)+2a^2=0\\ 0\le u\le\sqrt{a-\sqrt a}\\ \sqrt a\le v \le \sqrt{a+\sqrt a}. \end{cases} Solution $\mathbf{u+v=0}\ $ exists only if $\mathbf{a=0\Rightarrow x=0}.$
Solution $\mathbf{u+v\not=0}\ $ exists only if $\mathbf{a\ge1}$ and can be obtained from the system \begin{cases} (v-u)(2a-u^2-v^2)=1\\ 2(u^4+v^4) - 4a(u^2+v^2+1) + 4a^2=0\\ 0\le u\le\sqrt{a-\sqrt a}\\ \sqrt a\le v \le \sqrt{a+\sqrt a}.\tag6 \end{cases} wherein $\mathbf{u < v}.$
Taking in account the identity $$(2a-u^2-v^2)^2 = 4a^2 - 4a(u^2+v^2) + u^4 + v^4 + 2u^2v^2,$$ one can get the system \begin{cases} (v-u)(2a-u^2-v^2)=1\\ (2a-u^2-v^2)^2 + (u^2-v^2)^2 - 4a = 0\\ 0\le u\le\sqrt{a-\sqrt a}\\ \sqrt a\le v \le \sqrt{a+\sqrt a}, \end{cases} or \begin{cases} (v-u)(2a-u^2-v^2)=1\\ (v-u)^2((u^2-v^2)^2 - 4a) + 1=0\\ 0\le u\le\sqrt{a-\sqrt a}\\ \sqrt a\le v \le \sqrt{a+\sqrt a}.\tag7 \end{cases} Then \begin{align} &(u^2-v^2)^2= (v-u)^2(u+v)^2= (v-u)^2\biggl(2(u^2+v^2)-(v-u)^2\biggr)\\ &=(v-u)^2\biggl(2\left(2a-\dfrac1{v-u}\right)-(v-u)^2\biggr)\\ &=-(v-u)^4+4a(v-u)^2 - 2(v-u),\\ \end{align}
\begin{cases} (v-u)^6-4a(v-u)^4 + 2(v-u)^3 + 4a(v-u)^2 - 1=0\\ u^2+v^2=2a - \dfrac1{v-u}\\ 0\le u\le\sqrt{a-\sqrt a}\\ \sqrt a\le v \le \sqrt{a+\sqrt a}.\tag8 \end{cases}
$\color{brown}{\mathbf{\text{Getting of the possible solutions.}}}$
Formulas $(8)$ allow to get values $v-u = s$ and $u^2+v^2=2a-\dfrac1s$ by the given $a.$
The equation $$s^6 - 4as^4 + 2s^3 + 4as^2 - 1 = 0\tag9$$ can be solved, using the form of $$s^3 - \dfrac1{s^3} - 4a\left(s-\dfrac1s\right) + 2 = 0,$$ or $$4t^3+(3-4a)t-1 = 0,\tag{10}$$ where $$t=\dfrac12\left(\dfrac1s - s\right).$$ This gives the simple real solution
$$t = \dfrac12\left(\sqrt[3]{\sqrt{1+\left(1-\dfrac43a\right)^3}+1} + \dfrac{\dfrac43a-1}{\sqrt[3]{\sqrt{1+\left(1-\dfrac43a\right)^3}+1}}\right),\quad \mathbf{a\le\dfrac32}. \tag{11}$$
If $\mathbf{a>\dfrac32},$ then, using Chebyshev Polynomial of the First Kind, \begin{align} &4\left(\dfrac t{\sqrt{\dfrac43a-1}}\right)^3 - 3\left(\dfrac t{\sqrt{\dfrac43a-1}}\right) = \dfrac 1{\left(\sqrt{\dfrac43a-1}\right)^3},\\ \end{align} \begin{align} &\cos\left(3\arccos\left(\dfrac t{\sqrt{\dfrac43a-1}}\right)\right) = \dfrac 1{\left(\sqrt{\dfrac43a-1}\right)^3}, \end{align}
$$t = \sqrt{\dfrac43a-1}\cos\left(\dfrac{2k}3\pi + \dfrac13\arccos\dfrac1{\left(\sqrt{\dfrac43a-1}\right)^3}\right), \quad \mathbf{a>\dfrac32},\tag{12}$$
where $k=0,1,2$ is the branch number. That leads to the system $$\begin{cases} v - u = \sqrt{t^2+1}-t\\ u^2 + v^2 = 2a - \sqrt{t^2+1} - t. \end{cases}\tag{13}$$ At the same time, $$x=\dfrac{u+v}2 = \dfrac12\sqrt{2(u^2+v^2)-(v-u)^2}.$$ Therefore,
$$x = \dfrac12\sqrt{4a-2\sqrt{t^2+1}-2t-(\sqrt{t^2+1}-t)^2},\tag{14}$$
where $t$ is given by $(11),(12).$
$\color{brown}{\mathbf{\text{Solutions analysis.}}}$
Note that \begin{align} &\sqrt{a\mp x}=\sqrt a\sqrt{1\mp\dfrac xa}\ge \sqrt a\left(1\mp\dfrac x{2a}\right) = \sqrt a\mp\dfrac x{2\sqrt a}, \\[4pt] &\sqrt{a\pm\sqrt{a\mp x}} \ge \sqrt{a\pm\sqrt a - \dfrac x{2\sqrt a}} = \sqrt{a\pm\sqrt a}\sqrt{1-\dfrac x{2\sqrt a\left(a\pm\sqrt a\right)}}\\[4pt] &\ge \sqrt{a\pm\sqrt a}\left(1-\dfrac x{4\sqrt a\left(a\pm\sqrt a\right)}\right) = \sqrt{a\pm\sqrt a}-\dfrac x{4\sqrt a\sqrt{a\pm\sqrt a}},\\ &\sqrt{a+\sqrt{a-x}}+\sqrt{a-\sqrt{a+x}} \ge \sqrt{a+\sqrt a}+\sqrt{a-\sqrt a} - \dfrac x{4\sqrt a\sqrt{a-\sqrt a}\sqrt{a+\sqrt a}}\left(\sqrt{a+\sqrt a}+\sqrt{a-\sqrt a}\right) = \sqrt{2\left(a+\sqrt{a-a^2}\right)}\left(1-\dfrac x{4a\sqrt{a-1}}\right),\\ \end{align} $$\sqrt{a+\sqrt{a-x}}+\sqrt{a-\sqrt{a+x}} \ge \sqrt{2\left(a+\sqrt{a-a^2}\right)}\left(1-\dfrac x{4a\sqrt{a-1}}\right),\tag{15}$$ so the real solutions of the issue equation can exist only if $$1-\dfrac x{4a\sqrt{a-1}} \le\dfrac {2x}{\sqrt{2\left(a+\sqrt{a-a^2}\right)}}=\dfrac{\sqrt{2(a-\sqrt{a^2-a})}}{\sqrt a}x ,$$ or only in the case
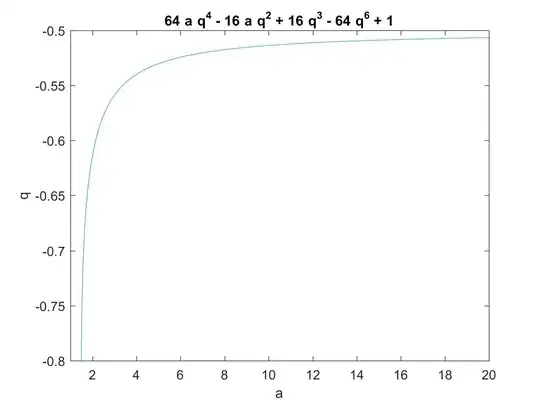
$$x\ge B(a),\quad B(a)=\dfrac{4a\sqrt{a-1}}{1+4\sqrt{2(a^2-a)(a-\sqrt{a-a^2})}}\tag{16}$$
(see also Wolfram Alpha)
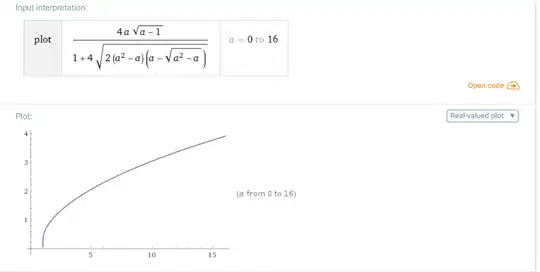
This means that solutions with $\mathbf{a<1}$ doesn't exist.
If $\mathbf{a\in\left[1,\dfrac32\right]},$ then solutions also doesn't exist.
In particular, for $a=\dfrac32\quad B(a)>0.86.$ On the other hand, equation $(10)$ takes form of
$$t^3-3t-1=0, \quad (t-1)(2t+1)^2=0,\quad t \in\{-1/2, 1\},\quad x \in\{\approx 0.732, 1/2\},$$
and this contradicts with $(16).$
Let us consider the case $\mathbf{a>\dfrac32}.$
If $\mathbf{k=0}$ (zero branch), then formula $(12)$ means that $$t\ge \sqrt{\dfrac43a-1}\dfrac{\sqrt3}2 = \sqrt{a-\dfrac34},$$ and one can check that $x(a)< B(a)$ (see also Wolfram Alpha).
If $\mathbf{k=1}$ (the first branch), then, using $(12),$ $$t\le -\sqrt{\dfrac43a-1}\dfrac{\sqrt3}2 = -\sqrt{a-\dfrac34},$$ and $x(a)<B(a)$ again (see also Wolfram Alpha).
If $\mathbf{k=2}$ (the second branch), then verification, using MathCad, leads to the positive result.
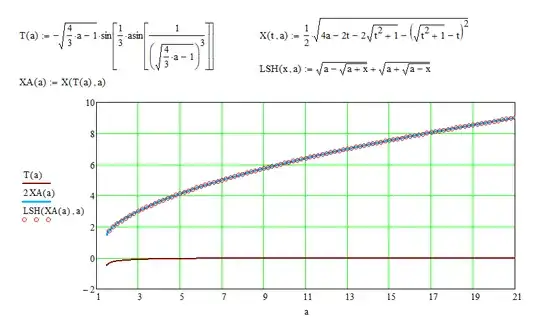
Therefore, all solutions $x$ of the issue equation can be defined by formula $(14),$ where
$$t=-\sqrt{\dfrac{4a-3}3}\sin\left(\dfrac13\arcsin\dfrac{3\sqrt3}{(4a-3)\sqrt{4a-3}}\right).\tag{17}$$
Gratitude to GCab to the solution example.
Squaring both sides, $$a\require{\cancel}\cancel{+\sqrt{a-x}}+a\cancel{-\sqrt{a-x}}+2\sqrt{\left(a+\sqrt{a-x}\right)\left(a-\sqrt{a-x}\right)}=2\left(a+\sqrt{a^2-a+x}\right)=4x^2.$$ since for all $m,n$ one has that $(m+n)(m-n)=m^2-n^2$. Now, dividing both sides by $2$,$$\begin{align} a+\sqrt{a^2-a+x}&=2x^2 \\ \Leftrightarrow (2x^2-a)^2 &= 4x^4 + a^2 - 4ax^2 \\ &= a^2 - a + x.\end{align}$$ Cancel out the term $a^2$ from both sides and expanding,$$4x^2(x^2-a) = x-a.$$ Now, notice that $$\frac{x^2-a}{x-a} = \frac{x^2-a+x-x}{x-a} = \frac{x^2-x}{x-a}+1.$$ Therefore, $$\begin{align}4x^2\left(\frac{x^2-a}{x-a}\right)= 4x^2\left(\frac{x^2-x}{x-a}+1\right)&=1 \\ \Leftrightarrow \frac{4x^3(x-1)}{x-a}+4x^2&=1.\end{align}$$ Now, since $4x^2 = (2x)^2$ then converting it to that and subtracting $1$ from both sides, $$\begin{align} \frac{4x^3(x-1)}{x-a} + (2x+1)(2x-1)&=0 \\ \Leftrightarrow \frac{4x^3(x-1)}{x-a} + x(2x+1) + (x-1)(2x+1) &= 0 \\ \Leftrightarrow (x-1)\left(\frac{4x^3}{x-a} + (2x+1)(x+1)\right)&=0.\end{align}$$ Solve for $x$ and $a$. To start you off, $x=1$.
