I ran across the following claimed explicit formula for $\Phi(x)$.
(1) $\quad\Phi(x)=\sum\limits_{n=1}^x\phi(n)$
(2) $\quad \frac{\zeta(s-1)}{\zeta(s)}=\sum\limits_{n=1}^\infty\frac{\phi(n)}{n^s}$
(3) $\quad\Phi_o(x)=\frac{3\,x^2}{\pi^2}+\sum\limits_{k=1}^K\left(\frac{x^{\rho_k}\,\zeta\left(\rho_k-1\right)}{\rho_k\,\zeta'\left(\rho_k\right)}+\frac{x^{\rho_{-k}}\,\zeta\left(\rho_{-k}-1\right)}{\rho_{-k}\,\zeta'\left(\rho_{-k}\right)}\right)+\frac{1}{6}+\sum\limits_{n=1}^N\frac{x^{-2\,n}\,\zeta(-2\,n-1)}{(-2\,n)\,\zeta'(-2\,n)}\,,\\$ $\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad K\to\infty\land N\to\infty$
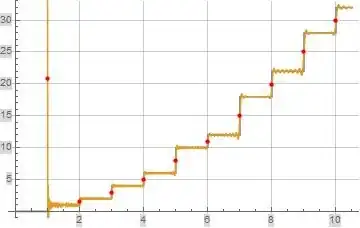
The formula for $\Phi_o(x)$ above doesn't seem correct as it only seems to converge for $x>1$ which is illustrated in the following plot of $\Phi_o(x)$ (orange) using the evaluation limits $K=N=200$. The $\Phi(x)$ function is shown in blue as a reference but is mostly hidden by the evaluation of $\Phi_o(x)$ except for $x<1$. The red discreet portion of the plot illustrates the evaluation of $\Phi_o(x)$ at integer values of $x$.
Question: What is the correct explicit formula for $\Phi(x)=\sum\limits_{n=1}^x\phi(n)$?
I realize the explicit formula for $\psi(x)$ only converges for $x>1$, but $\psi(x)$ doesn't take a step until $x=2$. Since $\Phi(x)$ takes a step at $x=1$, I was expecting the explicit formula for $\Phi(x)$ to converge for $x>0$ similar to the explicit formulas for $M(x)=\sum\limits_{n=1}^x\mu(n)$ and $Q(x)=\sum\limits_{n=1}^x\left|\mu(n)\right|$.