We have two kinds of Möbius strips.
Let $[0,1]\times[0,1]=\{(s,t)\mid 0\leq s,t\leq 1\}$. Then the quotient space $([0,1]\times[0,1])/\sim$ is a Möbius strip, where $(s,0)\sim(1-s,1)$.
Let $S^1\times S^1=\{(e^{2\pi is},e^{2\pi it}) \mid 0\leq s,t\leq 1\}$ be a torus. Then the quotient space $(S^1\times S^1)/\sim$ is a Möbius strip, where $(e^{2\pi is},e^{2\pi it})\sim(e^{2\pi it},e^{2\pi is})$.
[Reference] The accepted answer of "Orbit space of torus homeomorphic to mobius strip"
We want to find a parametrization $f\colon [0,1]\times[0,1]\to(S^1\times S^1)/\sim$ with two variables $(s,t)\in[0,1]\times[0,1]$.
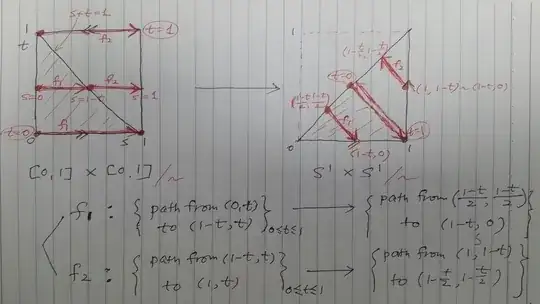
At first define $f_1\colon [0,1-t]\times[0,1]\to S^1\times S^1$ and $f_2\colon [1-t,1]\times[0,1]\to S^1\times S^1$ by
$$
\begin{cases}
f_1(s,t)=\left( e^{\pi i(1-t+s)}, e^{\pi i(1-t-s)} \right), & \text{$0\leq s\leq 1-t$} \\
f_2(s,t)=\left( e^{\pi i(3-t-s)}, e^{\pi i(1-t+s)} \right), & \text{$1-t\leq s\leq1$}
\end{cases} \tag{*}
$$
Then $f_1(1-t,t)=(e^{2\pi i(1-t)},1)\sim(1,e^{2\pi i(1-t)})=f_2(1-t,t)$. Attaching $f_1$ and $f_2$ along the line $s=1-t$ we have a continuous surjection
$$
f\colon [0,1]\times[0,1] \to (S^1\times S^1)/\sim
$$
Moreover, $f$ induces a homeomorphism between the two Möbius strips
$$
\tilde f\colon ([0,1]\times[0,1])/\sim \, \to (S^1\times S^1)/\sim
$$
since for all $0\leq s\leq1$,
$$
f(s,0) = f_1(s,0) = (e^{\pi i(1+s)},e^{\pi i(1-s)}) = f_2(1-s,1) = f(1-s,1)
$$
We can rewrite the parametrization (*) with 4-tuples as follows:
$$
\begin{align*}
f(s,t)=f_1(s,t) = \bigl( &\cos\bigl[\pi(1-t+s)\bigr], \sin\bigl[\pi(1-t+s)\bigr], \\
&\cos\bigl[\pi(1-t-s)\bigr], \sin\bigl[\pi(1-t-s)\bigr] \bigr)
\end{align*}
$$
for $0\leq s\leq 1-t$, and
$$
\begin{align*}
f(s,t)=f_2(s,t) = \bigl( &\cos\bigl[\pi(1-t-s)\bigr], \sin\bigl[\pi(1-t-s)\bigr], \\
&\cos\bigl[\pi(1-t+s)\bigr], \sin\bigl[\pi(1-t+s)\bigr] \bigr)
\end{align*}
$$
for $1-t\leq s\leq 1$.
Note that $f_1(s,t)$ is the same as $f_2(s,t)$ in the quotient space $(S^1\times S^1)/\sim$.
