Connect any three points using two parabolas

Question

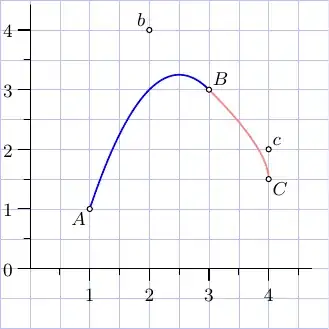
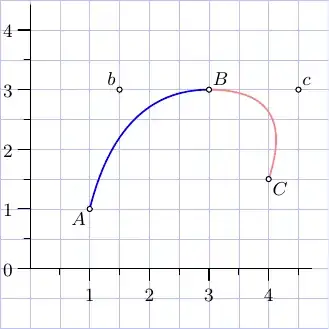
Let us say we have 3 points $(x_1,y_1),(x_2,y_2),(x_3,y_3)$. We want to build exactly 2 parabolas connecting theese points in a smooth way.

For the first parabola we can write system of two equations using known points $$y_1 = a_1 x_1^2 + b_1 x_1 + c_1$$ $$y_2 = a_1 x_2^2 + b_1 x_2 + c_1$$ Similarly for the second parabola we can do the same: $$y_2 = a_2 x_2^2 + b_2 x_2 + c_2$$ $$y_3 = a_2 x_3^2 + b_2 x_3 + c_2$$ But now we have 4 equations and 6 unknowns $( a_i,b_i,c_i)$, where $i=1,2$. We can write down an equation that meets the condition of the "smooth connection", i.e. derivative at the point $(x_2,y_2)$ is the same for parabola 1 and parabola 2: $$y_2^{'} = 2a_1 x_2 + b_1$$ $$y_2^{'} = 2a_2 x_2 + b_2$$ which leads us to the fifth equation: $2a_1 x_2 + b_1=2a_2 x_2 + b_2$

I can not find another one assumption that will make a number of unknowns even to a number of equations.

See an example of how it may look like.

Answer 1

We can use formulas for the quadratic Bezier spline segment

\begin{align} s(t,a,b,c)&=a(1-t)^2+2b(1-t)t+ct^2 ,\\ s'(t,a,b,c)&=2((b-a)(1-t)+(c-b)t) ,\quad t\in[0,1] . \end{align}

For the three points $A,B,C$ there are two segments $s_1(t,A,b,B)$, $s_2(t,B,c,C)$ with two control points $b,c$.

\begin{align} \text{Condition }\quad s_1'(1,A,b,B)&= s_2'(0,B,c,C) \\ \text{gives }\quad c &= 2\,B-b , \end{align}

hence we have one control point ($b$) to define the shape of this two-segment spline.

For example, choosing $b=(2,4)$ or $b=(1.5, 3)$ given $A=(1,1)$, $B=(3,3)$, $C=(4,1.5)$, we have two different splines:

Answer 2

Let there be three points $A,B$ and $C$. We note that the first parabola $S_1$ passes through the $A$ and $B$, and the other parabola $S_2$ passes through $B$ and $C$.

Now, recall that two points are not sufficient to determine a unique parabola, hence $S_1$ and $S_2$ both represent infinite parabolas (more accurately, a family of parabolas, all with two points common).

Obviously, since there are inifinte parabolas in $S_1$, infinite slopes are also possible at point $B$ for different parabolas at $S_1$. Now consider a parabola in $S_1$ with slope $m_1$, is it impossible to find another parabola in $S_2$ also with slope $m_1$ at point $B$? (hint: recall that $S_2$ is also an infinite set)

I hope that helps!

Answer 3

Suppose first that you're interested in parabolas of the form $y=f(x)$, as your question suggests. Then, given three points, there is a unique parabola passing through them. If you write the parabola in the form $y = ax^2 + bx + c$, then you can easily write down three equations (like the ones in your question), and use them to solve for $a$, $b$, $c$.

If you use two different parabolas of the form $y=f(x)$, with the same slope at the middle point, there are an infinite number of solutions to your problem. As you saw, you get five equations in 6 unknowns, which means that the solution has one unfixed degree of freedom. You could fix this degree of freedom in several ways. For example, you could specify the slope of the curve at the middle point. One way fix the degree of freedom is to require that the two parabolas have the same second derivative at the middle point. But, in fact, this will force the two parabolas to be the same, so we're back to the situation I discussed in the first paragraph.

Perhaps you're willing to use rotated parabolas, of the form $\mathbf{X}(t) = \mathbf{A}t^2 + \mathbf{B}t + \mathbf{C}$, where $\mathbf{A}$, $\mathbf{B}$, $\mathbf{C}$ are 2D vectors. You could regard these curves as quadratic Bezier crves. There are an infinite number of parabolas of this form passing through any three given points. This is discussed in this question.

Answer 4

I seem to understand that by "smoothtly" in this context you mean "with same first derivative": I believe the term is often taken to mean something more.

In any case, what leads you believe there should only be two parabolas satisfying your conditions? Not being able to find the siyth condition maybe perfectly reflects the problem, i.e. the fact you have an infinity of solutions.

As a note aside, please also be careful that your conditions allow for curves with "cusps". For example, the parabolic segment $y = x^2$ on the domain $[0,1]$ and the parabolic segment $ y = -x^2$ on the same domain: they go through the points $(1,1)$, $(0,0)$ and $(1,-1)$ and the derivative at $(0,0)$ is the same, yet I am not sure such a case falls in your definition of "smoothly".

EDIT

Let is assume you set the desired slope at the middle point. Then, for each parabola you have 3 conditions, just what you need to determine the parabola's equations: going through the two points and having the determined slope at the "connection" point. This suggests there is an infinity of soutios, which one can parametrise by the slope at the "connection" point.