What is exactly the test function in real analysis?

Question

I try to understand test functions to compare two functions $f_1$ and $f_2$ through integration. can someone explain test function to me simply? in other words, i want to understand the answer to my other question here.

Answer 1

A test function is (or can be) literally any function that is non-negative, smooth and with compact support. edit: non-negativity is optional, and there can be additional requirements as well but this is the spirit.

The name comes (as far as I know) from distribution theory: a distribution is a linear form on the space of test functions, and therefore you can tell two distributions apart by testing them (evaluating them) against test functions.

The first example of distribution that you ever meet is the integration over the real line of your test function times a fixed measurable function: $$\varphi \mapsto \int_\mathbb {R}f(t)\varphi(t) dt $$ This is pretty obviously a linear form, sort of dual to $ f $. You can use it to test $ f $, collect information about it.

How to think about this product $f\varphi$: since $\varphi$ has compact support, so does the product - everything outside the support is killed, and the value of the above integral gives you information about what $f$ does on the support of $\varphi$. You can be quite extreme in the way you localise, by having the support of $\varphi$ shrink to a single point. There is a quite instructive result as follows:

Theorem. If $f$ is a continuous map, and if $\varphi_k$ is a sequence of test functions whose support $[a_k, b_k]$ is such that $\lim a_k = \lim b_k = x$, and if $\int_\mathbb{R} \varphi_k =1$ for all $k$, then $$\lim \int_\mathbb{R} f\varphi_k=f(x)$$

All limits are for $k\to \infty$.

This tells you that you can recover completely the values of $f$ by testing it extremely locally. You can clearly see why the continuity of $f$ is necessary: otherwise the integral of $f$ would have nothing to do with the value it takes at a particular point.

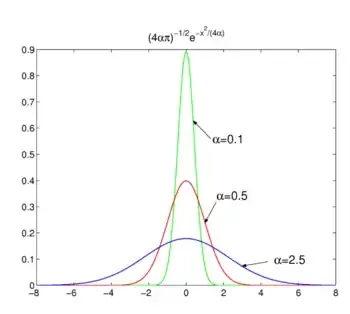
The $\phi_k$ in the above theorem can easily be achieved using Gaussians: