1

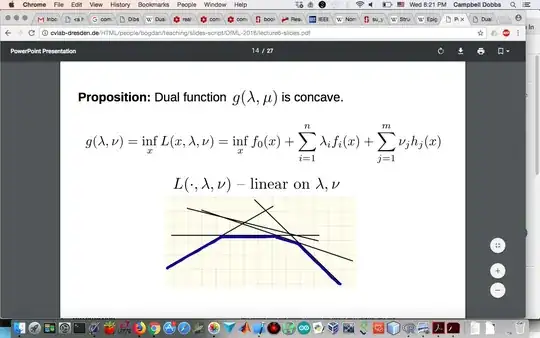
Wikipedia reads, "The dual function g is concave, even when the initial problem is not convex, because it is a point-wise infimum of affine functions." Can someone explain this? Maybe provide a basic example? What do they mean by "point-wise" and how does the point-wise infimum of affine functions imply concavity?

I've read similar posts about this on here but they use the same argument without an example or much of a proof.

Campbell
  • 105
  • What is the context of this quote? – saulspatz Jan 31 '18 at 23:51
  • Oh sorry, it's in the context of the Lagrangian dual function – Campbell Jan 31 '18 at 23:55
  • Let $f$ be a function. Presumably you're talking about the conjugate $g(y) := \inf_x f(x) - \langle y, x\rangle.$ Note that at each point $y,$ $g$ is an infimum over $x$ of the affine functions $g_x(y) :=f(x) - \langle y, x\rangle,$ and hence is a pointwise infimum. Note that since each $g_x$ is affine, it is also concave... – stochasticboy321 Feb 01 '18 at 00:13
  • ... (contd.) Now, a standard result is that the pointwise infimum of concave functions is concave. To see this, recall that the intersection of (any number of) convex sets is convex, and that a function is concave iff its hypograph is convex. But the hypograph of the infimum of a set of functions is the intersection of all the hypographs (Show this). – stochasticboy321 Feb 01 '18 at 00:14
  • A possible duplicate – A.Γ. Feb 01 '18 at 00:21
  • "since each gx is affine, it is also concave" - but isn't an affine function both concave and convex? – Campbell Feb 01 '18 at 01:08
  • And what is the infimum of a set of functions? If the functions are added together wouldn't this be a point? – Campbell Feb 01 '18 at 01:11
  • Ooh, I see now. Sorry, thanks, yeah the hypograph of the intersection of various affine functions' hypographs is obviously convex (hence the function is concave). – Campbell Feb 01 '18 at 01:29
  • Wait, no.. when you say "each gx" do you mean each gx for a given y? But that is just a point? – Campbell Feb 01 '18 at 01:57
  • ...because otherwise gx(y) is not affine necessarily, it is merely guaranteed to be concave. – Campbell Feb 01 '18 at 01:59

1 Answers1

2

I don't know why I couldn't see it initially but for any given $\lambda$ we have an affine function, x being constant so the basic idea is (just looking at the graph): enter image description here

wherein the "x-axis" is lambda and the "y-axis" is the value of the dual function g($\lambda$)

Campbell
  • 105