Chi-squared g00dness-of-fit (GOF) tests are widely used and often
misinterpreted. Here are two examples that involve testing to
judge whether a die is fair.
Example 1: Suppose we roll a die 60 times, and get the following
summary table of results.
face: 1 2 3 4 5 6
freq: 12 8 11 15 6 8
If the die is fair, then we say we would 'expect' each face to
occur 10 times. Of course, that would be an 'average' result.
In view of random variation, it would be a very rare outcome
to see a frequency of exactly 10 for each of the six faces.
The question is how much different from the 'expected' results
$E_i = 10$ can the actual results $X_i$ be before we reject the
null hypothesis that each face has probability $p_i = 1/6?$
The usual way to measure departure from the idealized outcome
is to compute the GOF statistic
$$Q = \sum_{i=1}^6 \frac{(X_i - E_i)^2}{E_i}.$$
For the data shown above, we have $Q = 5.4.$ Notice that if
all six observed frequencies were 10's, we would have $Q = 0,$
so large values of $Q$ correspond to poor fit to the null
hypothesis that the die is fair.
If the null hypothesis is true, $Q \stackrel{aprx}{\sim} \mathsf{Chisq}(\nu = 5),$
the chi-squared distribution with $\nu = 6 - 1 = 5$ degrees of
freedom. This is an approximation, but with all expected values $E_i > 5,$
some theory and some simulation studies show that the approximation is
good enough to use in testing the null hypothesis.
If we are testing the null hypothesis at the 5% level of significance,
the 'critical value' above which we reject the null hypothesis is
$c = 11.0705.$ Because $Q < c$ we do not reject the null hypothesis.
We say that the data are consistent with behavior of a fair die.
The value $c$ cuts 5% of the area from the upper tail of
$\mathsf{Chisq}(5).$
In R statistical software, the test procedure looks like this, where
face is the vector of the 60 outcomes tabled above. [Unless a vector
of probabilities other than $p = (1/6, 1/6, 1/6, 1/6, 1/6, 1/6)$ is
specified, the program assumes the 'given probabilities' are equally likely.]
chisq.test(table(face))
Chi-squared test for given probabilities
data: table(face)
X-squared = 5.4, df = 5, p-value = 0.369
The P-value is the probability a fair die would give a $Q$-value greater
than our result $Q = 5.4.$ [Another way to test at
the 5% level is to reject the null hypothesis if the P-value is smaller
than 5%.]
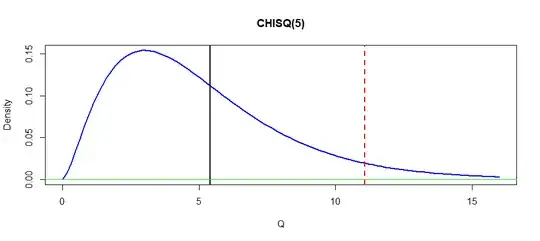
The figure below shows the density curve of $\mathsf{Chisq}(5).$ The
vertical dotted red line is at the critical value $c = 11.0705,$
the vertical solid black line is at the observed value $Q = 5.4,$
and the area beneath the curve to the right of the black line is
the P-value.
Example 2: By placing a lead weight beneath the corner of a die
where faces 4, 5, and 6 meet it would be possible to make an unfair die
with probabilities $$p = (7/36, 7/36, 7/36, 5/36, 5/36, 5/36).$$ With $n = 60$ rolls of such
an altered die, the
expected counts would be $$E = \left(11\frac23, 11\frac23, 11\frac23,
8\frac13, 8\frac13, 8\frac13 \right).$$
Now we ask whether our data are also consistent with 60 rolls of
such an unfair die. Again the 'null distribution' of $Q$ is
$\mathsf{Chisq}(5)$ and the critical value is $c=11.0705.$
However, we must use the new expected values $E_i$ in the
formula for the GOF statistic, so that $Q = 7.2 < c$ and
the null hypothesis is (once again) not rejected.
chisq.test(table(face), p=c(7,7,7,5,5,5)/36)
Chi-squared test for given probabilities
data: table(face)
X-squared = 7.2, df = 5, p-value = 0.2062
So we cannot say in Example 1 that we have "proved" the die is fair.
The data are also consistent with a die that is biased as described
in the current example. With only $n = 60$ rolls of the die,
we do not have enough information to distinguish between a fair
die and a somewhat biased one.
If the die were truly biased as described and the number of rolls had
been greater
(perhaps 600 instead of 60), then we would very likely get
data that are clearly not consistent with a fair die.
Note: The data for these examples resulted from 60 rolls of a
die that I suppose is fair. (Transparent plastic and no signs of
tampering.)
