7

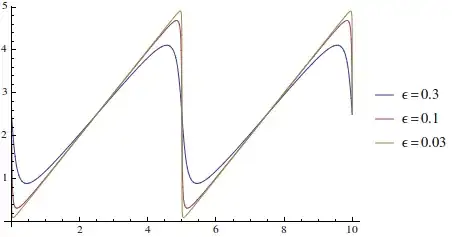
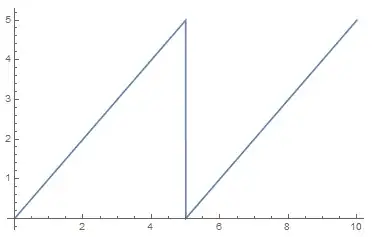
I'm looking for a function $m(x,y)$ that smoothly approximates $x \bmod y$, and I'm assuming there would be some $n$ or $\varepsilon$ in the body of $m(x,y)$ that defines the degree of approximation such that as $n$ goes to infinity or $\varepsilon$ goes to zero, $$ m(x,y)= x \bmod y. $$

I've looked at, for example, $\sin(x/y)$ and have been trying to figure out ways to make $\sin(x)$ more "steep" so that I can apply such techniques to $\sin(x/y)$ in order to perhaps more closely approximate $x \bmod y$.

The analogy I'm looking at is the approximation of $\mid x\mid$ as $\sqrt{x^2 + \varepsilon)}$ where epsilon is some small quantity.

Does a similarly smooth function exist for $x \bmod y$?

Noman
  • 99
  • 10
  • The edit looks nice but technically ruins your question. The function $m(x,y)=x$ satisfies the equation $m(x,y)\equiv x \pmod y$ for all integers $x$ and $y,$ but that "solution" is clearly not what you wanted. – David K Oct 26 '17 at 21:46
  • The way to format the operator you wanted is to write x \bmod y in MathJax; this typesets to "$x \bmod y$". It's a known, legitimate binary operator on two integers. – David K Oct 26 '17 at 21:48
  • Hmm, sorry I'm not so familiar with x (mod y) notation to be honest, so should I just revert to writing it out as I don't know latex either? – Noman Oct 26 '17 at 21:49
  • I think it is what you want now. No need to revert back to plain text. – David K Oct 26 '17 at 21:55
  • Nvm, thanks for the tip, the question's updated. – Noman Oct 26 '17 at 21:56
  • Now I just need to go think about the actual question a bit ... :-) – David K Oct 26 '17 at 21:57

4 Answers4

7

Let $\theta=\pi x/y$. @user2249675's answer involves a term $\cot\theta=\cos\theta/\sin\theta$. We can construct a smooth approximation by replacing $1/\sin\theta$ with $\sin\theta/(\sin^2\theta+\epsilon^2)$, giving the final answer $$m(x,y)=y\left(\frac12-\frac1\pi\arctan\left(\frac{\cos(\pi x/y)\sin(\pi x/y)}{\sin^2(\pi x/y)+\epsilon^2}\right)\right).$$

Here is a plot with $y=5$:

enter image description here

4

Here's a simple answer you can try: $$m(x,y) = y\left(\frac{1}{2} - \frac{\arctan(\cot(\pi x/y))}{\pi}\right)$$ Plot with $y = 5$:

enter image description here

user2249675
  • 1,165
  • 3
    The question asked for "smooth". I don't know if it really meant smooth in the mathematical sense, but this function isn't even continuous. – David K Nov 14 '17 at 04:02
3

I think the fourier series for the sawtooth wave might be helpful here.

http://mathworld.wolfram.com/FourierSeriesSawtoothWave.html

The series is given by

$$x=\frac{L}{2}-\frac{L}{\pi}\sum_{n=1}^\infty\frac{1}{n}\sin\frac{2n\pi x}{L},\quad x\in(0,L).$$

If $x\notin(0,L)$, the Fourier series gives $x\mbox{ mod } L$, which is what is wanted here. Truncating at finite order gives a continuous approximation of $x\mbox{ mod }L$.

Zhuoran He
  • 3,149
  • 1
    Though the Gibbs phenomenon would mean the partial sums won't converge uniformly to the sawtooth function, which may or may not make it unsuitable for the OP's purposes. – Daniel Schepler Oct 26 '17 at 22:32
1

One approach I found was to find a smooth floor function, and then simply apply it to the equation:

$$ x \bmod y=x-{\lfloor}\frac{x}{y}{\rfloor}y $$

And a definition for the smooth floor function I derived is:

$$ {\lfloor}x{\rfloor}=-\frac{1}{2} + x + a ln(1/a) -\frac{i}{2 \pi} \left[ln\left(1-e^\left(-2 i \pi \left(x+a ln(1/a)\right)\right)+a\right) - ln\left(1-e^\left(2 i \pi \left(x+a ln(1/a)\right)\right)+a\right) \right] $$

As you make a smaller and smaller, this increasingly approximates the floor function.

Update

I realized after posting that @user856 had already posted a much simpler approximation quite a while ago.

Noman
  • 99
  • 10