Efficiently generate a sawtooth with rounded peaks.

Question

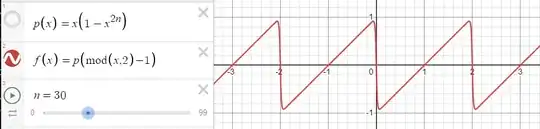
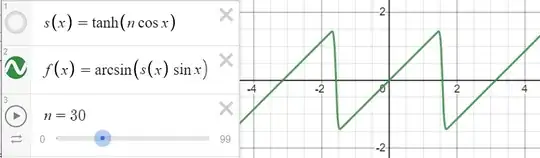
I'd like to have an efficient function that would generate a wave that is close to a sawtooth but has slightly rounded peaks. The wave needs to be continuous at all points. I will be doing this in directx and opengl shaders so I have access to vector units and matrix multiplies.

EDIT: I can efficiently generate a sawtooth with the following line of code: (assuming t [0,1])

saturate(t*10.0) - t;

The problem with this is that the line isn't continuous. I'm considering sampling 4 points on the line (2 before t and 2 after) and then doing a Catmul Rom spline, but I'd be interested in any suggestions for a better way to do the smoothing.

Why don't you generate a function for a sawtooth on a closed interval, then Fourier transform it? — Rushabh Mehta, Oct 05 '18 at 16:04
If it's a periodic function, definitely consider the Fourier series — Vasili, Oct 05 '18 at 16:07
I wouldn't think that fast Fourier transforming it would be very fast. (I could be wrong, I'm not very knowledgeable about how to implement a fft) — Chip Burwell, Oct 05 '18 at 16:20
If the function is periodic and fixed you could define one period of the function and save in memory. — overfull hbox, Oct 05 '18 at 16:43
What about this https://math.stackexchange.com/questions/2430564/equation-of-a-tilted-sine ? — cgiovanardi, Oct 09 '18 at 13:21
Related: Does there exist a smooth approximation of x mod y? — Ruud Helderman, Jan 17 '25 at 13:59

Ruud Helderman · Accepted Answer · 2022-08-09T19:23:03.967

3

The following polynomial gives a single 'tooth' on domain $[-1, 1]$. The higher $n$, the sharper the peak.

$$ p\left(x\right)=x\left(1-x^{2n}\right) $$

Repeat the function to extend the domain to $\mathbb{R}$:

$$ f\left(x\right)=p\left(\left(x\bmod 2\right)-1\right) $$

A screenshot from Desmos:

Note: $f$ and $f'$ are continuous, but the second derivative is not continuous.

As for efficiency: $n$ is integer, so $x^{2n}$ can be calculated with a sequence of $\mathcal{O}(\log n)$ multiplications.

edited Aug 09 '22 at 19:23

answered Aug 09 '22 at 18:37

Ruud Helderman

166

Four year old question gets a good answer. Neat! – Chip Burwell Aug 10 '22 at 19:52

Ruud Helderman · Answer 2 · 2022-08-13T08:02:47.217

In case anyone needs a smooth sawtooth function that is infinitely differentiable ($C^{\infty}$): there are various ways to construct such a function, typically by combining trigonometric functions.

One way is to start with a smooth square wave like:

$$ s\left(x\right)=\tanh\left(n\cos x\right) $$

or:

$$ s\left(x\right)=\frac{2}{\pi}\arctan\left(n\cos x\right) $$

(the higher $n$, the sharper the edges)

Let the square wave flip a triangle wave to produce a sawtooth:

$$ f\left(x\right)=\arcsin\left(s\left(x\right)\sin x\right) $$

Screenshot from Desmos:

Obviously, this is likely to be more computationally expensive than the polynomial in my other answer. But that one, being a piecewise function, offers only $C^{1}$ continuity.

Other suggestions can be found here: https://mathematica.stackexchange.com/q/38293

Efficiently generate a sawtooth with rounded peaks.

2 Answers2