Plugging a circle into real polynomial

Question

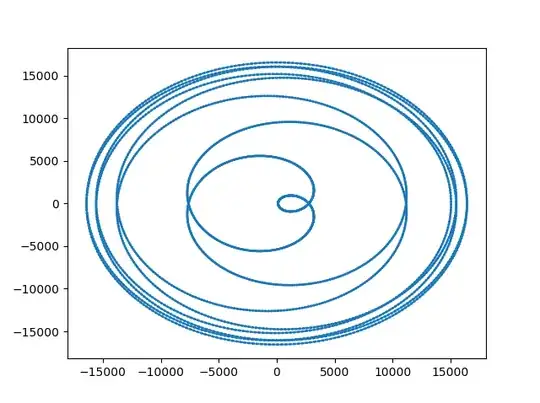
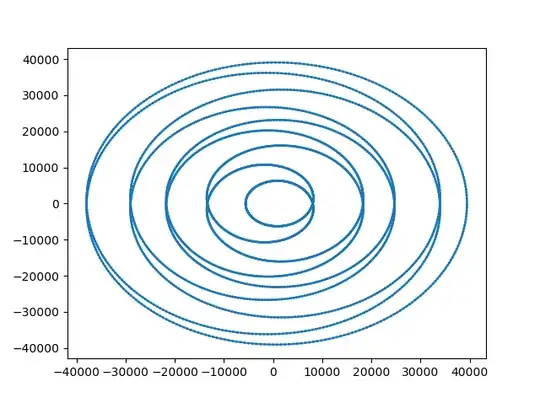
I have written some code (attached below) that generates a random real polynomial $P$ degree and coefficient within some range. I then plotted and looked at $im(P(S^1)) $ with $S$ being the unit circle in the complex plane.

To my surprise I got pictures with some interesting properties. (Interesting at least for me, (pictures are viewable below))

I noticed:

The figure is connected (not too surprising)
The figure is self-intersecting itself and an intersection seems to be always crossed exactly twice. (Might be wrong, considering rounding errors etc.)
The intersection points $z_i$ seem to have Im$(z_i) = 0$

Point 1. follows directly from S being compact and $P$ continuous. However I find it harder to justify 2 and 3, especially I can make such a claim, maybe I were just lucky with my numbers. Therefore I would appreciate it, if someone could clarify points 2 and 3 to me, if those statements are correct and especially why. As always thanks in advance.

'''
Created on 16 Sep 2017

@author: Imago
'''
import pylab
import cmath as c
import matplotlib.cm as cm
import matplotlib.pyplot as plt
import numpy as np
import random as r

NUMBER_OF_POINTS = 0.0001
RADIUS = 2.8

N = NUMBER_OF_POINTS
R = RADIUS

# generate a random polynominal with degree deg, and integer coefficients in range (min, max)
def grp(min, max, deg):
    l = list()
    for i in range(deg):
        l.append(r.randint(min, max))
    return np.poly1d(np.array(l))

# give me Re(z), Im(z)
def split(z):
    return complex(z).real, complex(z).imag

# my polynominal
f = grp(-3, 3, 10)
print('Polynominal')
print(f)

# interval of numbers between 0 and 1.    
I = np.arange(0, 1, N)

# skip the next 6 lines, if you not want to expande the code
X = list()
Y = list()
n = 1
k = 0
X.append(list())
Y.append(list())

# create the points for plotting
for x in I:
    z = R * np.exp(x * 2 * np.pi * 1j)
    v = f(z)
    X[k].append(complex(v).real)  # k = 0
    Y[k].append(complex(v).imag)

# colour, plot and show the figure
colors = iter(cm.rainbow(np.linspace(0, 1, n)))  # n = 1
for c in colors :
    plt.scatter(X[k], Y[k], c)
    k = k + 1
plt.show()

Beautiful and engaging stuff stuff! A couple of remarks:: *(i.): in the text, you refer to looking at $im P(S)$; I guess that means the image or $S$ under $P$, right? I first thought it meant the imaginary part of $P(S)$, but that doesn't seem right . . . ; (ii.)* it might be very helpful to those of us who find your work engaging if you reported the degrees and coefficients of the polynomials you used; it looks to me at first glance like your codes reports this information. Looking forward to hearing form you again . . . I may have more questions later on . . . Cheers! — Robert Lewis, Sep 16 '17 at 20:44

score 3 · Answer 1 · answered Sep 16 '17 at 17:57

Ad 2: A polynomial with threefold intersection would be $$f(x)=(x^3-1)x.$$

Ad 3: It is clear that the image is symmetric with respect to the $x$-axis, which automatically causes intersection points there as soon as the curve crosses the $x$-axis non-perpendicularly. Nevertheless, $f(x)=x^2$ can be said to pass twice hrough each of its point (even though this might be considered cheating). Maybe try $$ f(x)=x^3+(x^{9}-1)x$$

Plugging a circle into real polynomial

1 Answers1