Differences between homography and transformation matrix

Question

I'm wondering whats the differences between a homography and a transformation matrix?

For me it's kinda look like the same? Or is homography just the more precise word in the area of computer vision and transformation of image plane?

Answer 1

The term homography is often used in the sense of homography matrix in computer vision. In maths, I guess, the term homography describes the substatial concept, not the matrix. So the question is: What is the difference between homography matrix and transformation matrix?

The mathematical name for homography concept is "projective transformation" (source) and in computer vision it refers to transforming images such as if they were taken under different perspective. This is a much narrower question than any arbitrary transformation and hence homography can be computed by using mathematical tricks (see this question for details), avoiding geometrical computations. The effect of applying the matrix should be the same, but the way to get this matrix is easier.

An example from opencv: we have two images of the same place, taken from different angle. We will compute homography H. If we now select one pixel with coordinates (x₁, y₁) from the first image and another pixel (x₂, y₂) that represents the same point on another image, we can transform the latter pixel to have the same viewing perspective as the first one by applying H:

As we see, it is identical to applying transformation matrix, hence homography is just a special case of transformation. Most examples that I have seen, consider homography only for 2D (i.e., for images). Still, homography can be extended to larger dimension (source). Thanks to homography, 3D to 2D planar projection (i.e., mapping coordinates in 3D space to points on 2D plane) reduces to 2D to 2D, i.e., to a less complex problem (source).

While transformation is very general concept and includes all kinds of conversions, including conversion between coordinate frames, homography is a subset of it, mostly only applied when rotation is needed (source). In computer vision it is a technical term that describes above-mentioned case of transformation. You can achieve the same result by using proper geometrical transformation, but it will be more complex.

Answer 2

MF.OX's answer still leaves some points of wonder:

Is a homography constrained in some way, or can any matrix ($3\times3$) be a homography matrix in homogeneous 2d space?

I found out that yes, a homography matrix's elements are unconstrained - and it is synonymous to a projectivity. To answer the question of what a homography actually is, it is useful to compare the concept of a homography also to Affinity, Similarity, Euclidean Transforms, etc. Those are all constrained more strongly, so the word homography is useful to explicitly state that the matrix may not adhere to those stronger constraints.

To this purpose, I find this comparison useful:

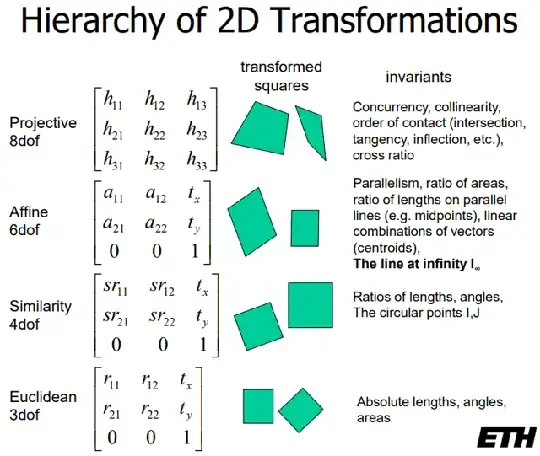
Source: https://www.cvg.ethz.ch/teaching/3dvision/2020/slides/class02eth20.pdf

So a "transformation matrix" is a general term and a "homography" is technically the same, but I believe it is used mainly to point out that there are no further constraints. That is, I would not say that an Affine Transformation is a Homography when I know that it is always affine. But I would call an Affine Transformation a Transformation - like wikipedia does here, for example.