An amazing property of the Catenary

Question

I discovered that if we want an arc of catenary in the interval $[a,b]$ we solve $$\int_a^b \sqrt{\cosh '(x)^2+1} \, dx=\int_a^b \cosh x \, dx$$ which means that the "result" of the length is equal to the result of the area in the same interval, though in different units.

So I asked myself if there are any other curve with the same property.

I set $$y=\sqrt{y'^2+1}\to y^2=y'^2+1; y(0)=1$$ then $$y'=\sqrt{y^2-1}\to dx=\frac{dy}{\sqrt{y^2-1}}\to x=\cosh^{-1} \,y$$ hence, arbitrary constant is zero, $y=\cosh x$

But I am not sure how to deal with the other solution $y'=-\sqrt{y^2-1}$ even if Mathematica gives the same result $y=\cosh x$

I'd like someone checking this proof, you know: I am not a pro, I am just an (almost) retired high school teacher :)

Update 9/1/2020. Now I am officially retired :)

Answer 1

EDIT1:

I understood your question in this way:

How is it that the area under a Catenary is proportional to the arc length? i.e., how is $$ c=\dfrac{A}{L}$$ valid for some constant of proportionality $c$?

At first about the sign in front of radical sign in DE

Let us at the outset consider very familiar similar situations:

If two DEs are given as $$ y'= + \sqrt {1-y^2},\; y'= - \sqrt {1-y^2} $$

we have in either case by squaring $$ y^{'2} = (1-y^2) $$

Differentiate

$$ 2 y' y^{''}= -2 y y',\to y^{''}+y =0 $$ which is the differential equation of a sine curve.

With BC $ x=0,y=1,y'=0 \to y= \cos x $ in either case

Similarly if two DEs are given as

$$ y'= + \sqrt {y^2-1},\; y'= - \sqrt {y^2-1} $$

we have in either case

$$y^{'2}= (y^2-1)$$

Differentiating

$$ 2 y' y^{''}= 2 y y',\to y^{''}-y =0 $$ which is the differential equation of a Catenary. With BC $ x=0,y=1,y'=0 \to y= \cosh x $ in either case.

However, if you do not wish to square thereby losing its sign but wish to directly integrate the two BCs, the following:

$$ y'= + \sqrt {1-y^2},\; y'= - \sqrt {1-y^2} $$

we get

$$ \sin^{-1}y= x +c_1, \sin^{-1}y=- x-c_2 $$

$$y= \sin (x+c_1),y= -\sin (x+c_2)$$

For (an even ) a symmetric solution $ x=0, y=1 $ we have respectively

$$c_1=\pi/2, c_2= 3 \pi/2$$

both yielding the same solution

$$ y = \cos x $$

When we have here our actual case

$$ y'= + \sqrt {1+y^2},\; y'= - \sqrt {1+y^2} $$

we get

$$ \cosh^{-1}y= x +c_1, \cosh^{-1}y=- x-c_2 $$ $$y= \cosh (x+c_1),y= \cosh (x+c_2)$$

For even symmetric solution $ x=0, y=1 $ we have respectively

$$c_1= c_2= 0 $$

yielding both the same solution

$$ y = \cosh x $$

So we can say in conclusion that in front of any (square root) radical sign we have $\pm$ and both signs are equally applicable for first order DE. It is only by a convention that we put in a positive sign implying the unsaid negative. They result in the same differential equation and hence also the same integrand for given boundary conditions in this particular case.

Geometrically a negative or positive sign of derivative relates to different slopes of the curve in different portions of the curve.

Next to answer what I considered to be your main question let us set up its DE which uniquely defines the curve.

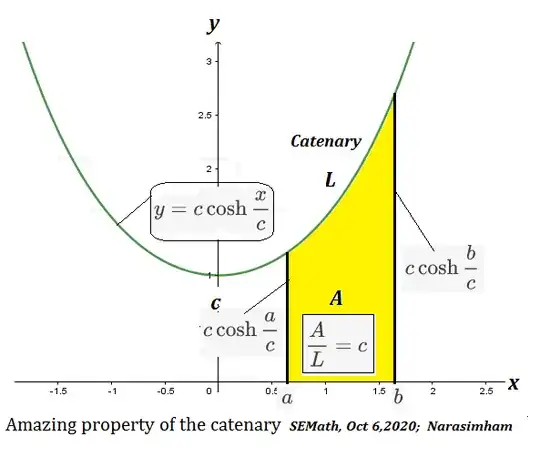
To get a physical/geometrical idea a length dimension quantity $c$ is introduced as the quotient of covered area $A$ to the length of its curved "roof".

$$c=\dfrac {\int y \; dx}{\int\sqrt{1+y'^2}dx}$$

Using Quotient Rule differentiate to simplify

$$c=\dfrac{ y} {\sqrt{1+y'^2}}= \to y' = \dfrac{\sqrt{y^2-c^2}}{c} $$

which is the differential equation of the unique curve being sought.

Integrating with boundary condition $ y(0)=c ,y'(0)=0,$ one obtains the equation of the only curve that satisfies the required property.

$$ \dfrac{y}{c}= \cosh\dfrac{x}{c}$$

which is recognized as a catenary as stated. And in association this property is recognized as well... that $c$ is the constant of proportionality which is the minimum distance of the catenary to the x-axis.

$$ c=\dfrac{A}{L}$$

as also shown here graphically.

Answer 2

From

$$\frac{y'}{\sqrt{y^2-1}}=\pm1$$ you draw

$$\text{arcosh}(y)=c\pm x$$

and

$$y=\cosh(c\pm x).$$

With the initial condition $y(0)=1$,

$$y=\cosh(\pm x)$$ which is $$y=\cosh(x).$$