21

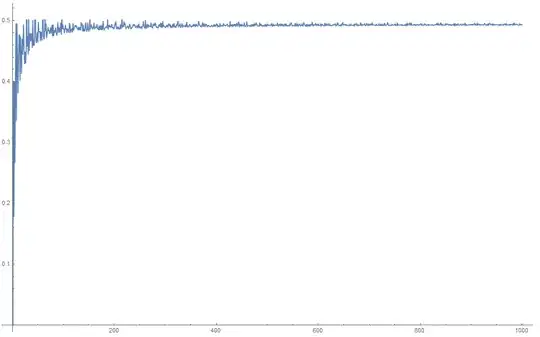
$\newcommand{\P}{\operatorname{P}}$I'm wondering if this sum of prime numbers converges and how can I estimate the value of convergence.

$$\sum_{k=1}^\infty \frac{\P[k+1]-2\P[k+2]+\P[k+3]}{\P[k]-\P[k+1]+\P[k+2]}$$

$ \ $

\begin{align} \sum_{k=1}^{10} \frac{\P[k+1]\cdots}{\P[k]\cdots} & = 0.4380952380952381` \\ & \,\,\, \vdots \\ \sum_{k=1}^{10^5} \frac{\P[k+1]\cdots}{\P[k]\cdots} & =0.49433323447491884` \\[10pt] \sum_{k=1}^{10^6} \frac{\P[k+1]\cdots}{\P[k]\cdots} & = 0.49433634247938607`\ \approx \frac{5}{7}\zeta(3)^{-2} \end{align}

$\ $

$ \zeta(s) \ $ is the Reimann zeta function

P$[n] \ $ is the $n^\text{th}$ prime number

$\ $ enter image description here

This is enough to assert that the series converges?

How can I estimate the value of convergence and if it is rational or irrational?

Patrick Danzi
  • 1,589
  • 11
    How did you manage to conjecture $5/7 \zeta(3)^{-2}$ ? – Zubzub Jun 16 '17 at 17:03
  • 2
    Where does this sum arise? Replacing $p_n$ with $n\ln n$ I believe the terms are bounded by $\frac 1{k\ln k}$ which would imply convergence. (Note I did it too quickly to be confident and one would need to check that it's ok to simply use the prime number theorem estimate.) – lulu Jun 16 '17 at 17:20
  • @lulu I was looking at the gap between two prime numbers and I was wondering if it was to look for the link between the first number n and the number n + 1, it would be more predictable to take into account also the following n+2, n+3 numbers – Patrick Danzi Jun 16 '17 at 17:42

2 Answers2

11

As I commented on @user1952009's answer, the series converges under assumption of Cramer's conjecture. However, we can prove the convergence of the series unconditionally. We have in fact a result on partial sums of squares of prime gaps which was proven by R. Heath-Brown. Here's the link to the paper:

Theorem [Heath-Brown]

Let $p_n$ be the $n$-th prime, and let $g_n = p_{n+1}-p_n$. Then we have $$ \sum_{n\leq x} g_n^2 \ll x^{\frac{23}{18}+\epsilon}. $$

After @user1952009's answer, it suffices to consider the convergence of (1): which is $$ \sum_{k=2}^{\infty} \frac{g_k g_{k+c}}{k^2 \log^2 k} < \infty. $$

Note that $2g_kg_{k+c}\leq g_k^2 + g_{k+c}^2$, so it suffices to consider the convergence of $$ \sum_{k=2}^{\infty} \frac{g_k^2}{k^2\log^2 k} $$ since the same idea will apply to $\sum_{k=2}^{\infty} \frac{g_{k+c}^2}{k^2\log^2 k}$. Let $A(x)=\sum_{k\leq x} g_k^2$, $f(x) = \frac1{x^2 \log^2 x}$. Heath-Brown's result states $A(x) \ll x^{23/18+\epsilon}$. Then by partial summation, we have $$ \begin{align} \sum_{2\leq k\leq x} \frac{g_k^2}{k^2\log^2 k}&=\int_{2-}^x f(t) dA(t) \\ &=f(t)A(t) \bigg\vert_{2-}^x -\int_{2-}^x A(t) f'(t)dt\\ &=f(2-)A(2-) + O\left( x^{-\frac{13}{18}+\epsilon} \right)+\int_{2-}^x \frac{2A(t) (\log t + 1) }{t^3\log^3 t}dt \end{align} $$ Now, we have the convergence since $23/18 - 3 = -31/18<-1$.

Another problem that uses Heath-Brown's result is here.

Sungjin Kim
  • 20,850
9

Letting $b_k = p_k - p_{k+1}+p_{k+2}$ and $a_k = g_{k+2} - g_{k+1}$ where $g_k = p_{k+1}-p_k$,

summing by parts $$\sum_{k=1}^n \frac{a_k}{b_k} = \frac{g_2-g_{n+2}}{b_n}+\sum_{k=1}^{n-1} (g_2-g_{k+2})(\frac{1}{b_k}- \frac{1}{b_{k+1}})$$ Since $b_k \sim k \log k$ $$\frac{1}{b_k}- \frac{1}{b_{k+1}}= \frac{b_k-b_{k+1}}{b_kb_{k+1}}\sim \frac{g_k+g_{k+1}+g_{k+2}}{k^2 \log^2 k}$$ Also we know $g_k = \mathcal{O}(k^\theta)$ for some $\theta < 0.6$ but this is not sufficient to conclude.

We look instead at $$\sum_{k=2}^\infty \frac{g_k g_{k+c}}{k^2 \log^2 k} \overset{?}< \infty \tag{1}$$

By summation by parts $\sum_{k=2}^K \frac{g_{k+c}}{k \log k} \sim \log K$ so I'd say yes $\sum_{k=2}^\infty \frac{g_k g_{k+c}}{k^2 \log^2 k}$ converges, but I can't prove it.

Summing by parts $\sum_{k=K}^\infty \frac{g_k }{k^2 \log^2 k} \sim \frac{1}{k \log k}$ lets me think $(1)$ converges.

reuns
  • 79,880