A way to solve the gap between prime numbers

Question

Some time ago I found this sum of prime numbers converge(*)

$$\sum_{k=1}^\infty \frac{p(k+1)-2p(k+2)+p(k+3)}{p(k)-p(k+1)+p(k+2)}\ \approx \frac{5}{7}\zeta(3)^{-2} $$ where:

$\zeta(s)$ is the Riemann zeta function

$p(n)$ is the $n^{th}$ prime number

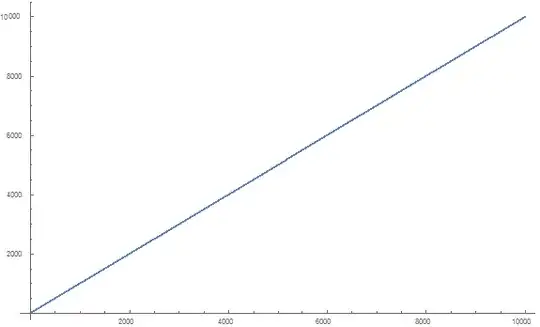
Working a bit on I found that: $$\sum_{k=1}^n \frac{p(k+1)-p(k+2)+p(k+3)-p(k+4)+p(k+5)}{p(k)-p(k+1)+p(k+2)-p(k+3)+p(k+5)}\ \approx n $$

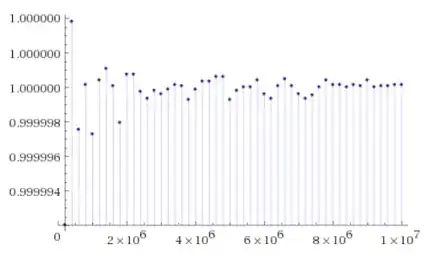
this means that $$F(k)=\frac{p(k+1)-p(k+2)+p(k+3)-p(k+4)+p(k+5)}{p(k)-p(k+1)+p(k+2)-p(k+3)+p(k+5)}\approx 1$$

$F(k):$

$F(k)=1 \pm \varepsilon_{n}$

$p(k+1)-p(k+2)+p(k+3)-p(k+4)+p(k+5)=p(k) \pm \varepsilon_{n}p(k)-p(k+1)\pm \varepsilon_{n}p(k+1)+p(k+2)\pm \varepsilon_{n}p(k+2)-p(k+3)\pm \varepsilon_{n}p(k+3)+p(k+5)\pm \varepsilon_{n}p(k+5).$

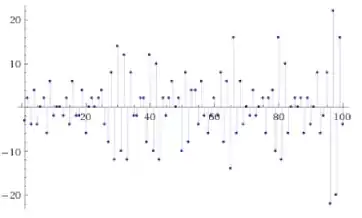
$E_k=\pm\varepsilon_n(p(k)+p(k+1)+p(k+2)+p(k+3)+p(k+5))$

$ \ $

$$p(k+4)=2p(k+3)-2p(k+2)+2p(k+1)-p(k)+E_{k}$$

$E_{k}:$

In this way you can look for the next prime number taking into account the error $E_{k}$.

How can I calculate the range of $E_{k}$?

I do not know if this way has already been used by someone, I had the pleasure of sharing it because of my lack of mathematical knowledge I would not know how to go on

(*)Does this sum of prime numbers converge?

Answer 1

Unfortunately, this answer deals more with approximations than bounds, but it should have a lot of useful information. I will use two approximations throughout this answer $$\begin{align}p(k)&\approx k\ln k&\text{(Prime Number Theorem)}\\ \ln(k+1)-\ln k&\approx\frac1k&\text{(Approximation from Derivative)} \end{align}$$ More specifically, $$\frac1{k+1}<\ln(k+1)-\ln k<\frac1k$$

$$F(k)=\frac{p(k+1)-p(k+2)+p(k+3)-p(k+4)+p(k+5)}{p(k)-p(k+1)+p(k+2)-p(k+3)+p(k+5)}\approx 1$$ Now, I will deal with the numerator of $F(x)$ first. At times, this may be hard to follow because of the sheer number of terms, so I will use colors to differentiate them. $$N=\color{red}{p(k+1)}-\color{orange}{p(k+2)}+\color{green}{p(k+3)}-\color{blue}{p(k+4)}+\color{purple}{p(k+5)}\approx \color{red}{(k+1)\ln(k+1)}-\color{orange}{(k+2)\ln(k+2)}+\color{green}{(k+3)\ln(k+3)}-\color{blue}{(k+4)\ln(k+4)}+\color{purple}{(k+5)\ln(k+5)}$$ Regrouping terms yields $$k\color{red}(\ln(k+1)\color{blue}{-\ln(k+2)+\ln(k+3)}\color{green}{-\ln(k+4)+\ln(k+5)}\color{red})+\ln(k+1)-2\ln(k+2)+3\ln(k+3)-4\ln(k+4)+5\ln(k+5)$$ $$k\ln (k+1)+k\left(\color{blue}{\frac1{k+2}}+\color{green}{\frac1{k+4}}\right)-\frac1{k+1}+\frac1{k+2}-\frac2{k+3}+\frac2{k+4}+3\ln(k+5)$$ The five rightmost terms may be hard to understand, but they are found by the same process with which we found the blue and the green terms, using the second approximation. More algebraic simplification yields $$k\ln(k+1)+3\ln(k+5)+\frac{k+1}{k+2}+\frac{k+2}{k+4}-\frac1{k+1}-\frac2{k+3}$$ Now for the denominator, I use the same exact process, so I won't waste space by going through it again. $$D=p(k)-p(k+1)+p(k+2)-p(k+3)+p(k+5)\approx k\ln k+3\ln(k+5)+\frac{k+2}{k+4}+\frac{k+2}{k+3}-\frac1{k+2}+1$$ The approximation for $p(k+4)$ is $$p(k+4)\approx k\ln(k+1)+3+2\ln(k+3)+2\ln(k+1)+E_k$$ Now, we know $E_k=\varepsilon_n\cdot D$, but we also know $\frac ND=1\pm\varepsilon_n$, which means $N=D\pm\varepsilon_n\cdot D\implies|\varepsilon_n\cdot D|=|N-D|$ By the same process we used to find the numerator, $$|\varepsilon_n\cdot D|=|N-D|=\frac1{k+1}+\frac1{k+3}$$ We can now write the approximation as $$p(k+4)\approx k\ln(k+1)+3+2\ln(k+3)+2\ln(k+1)\pm\left(\frac1{k+1}+\frac1{k+3}\right)$$ Now, replacing $k$ with $k-3$ to get an approximation for $p(k+1)$ yields. $$p(k+1)\approx k\ln(k-2)+3+2\ln k-\ln(k-2)\pm\left(\frac1{k-2}+\frac1{k}\right)$$