Exploring Properties of Pascal's Triangle $\pmod 2$

Question

Moderator Note: This question is from a contest which ended 1 Dec 2012.

Consider Pascal's Triangle taken $\pmod 2$:

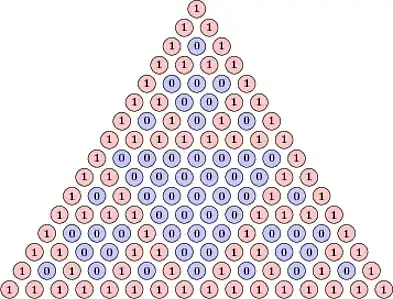
First few rows of Pascal's Triangle modulo 2

For simplicity, we will call a finite string of 0's and 1's proper if it occurs in one of the rows of this modified Pascal's triangle. (for example, 0 (row 3) and 10001 (row 5) are proper).

I've been exploring proper strings of length $n$. My professor told me it is possible to

i) characterize explicitly all proper strings of length $n$

and ii) Find an explicit formula for the number of proper strings of length $n$.

But I cannot figure out how to even begin either parts. This is a very interesting problem, and I was wondering if someone could help me. Thank you!

I would start by trying to answer the question for small values of n. — Jonah Sinick, Nov 05 '12 at 00:54
This may be a silly question, but can you see any strings which are not proper? — JavaMan, Nov 05 '12 at 03:34
The numbers seem to satisfy A014206, but the strings themselves are not bitonic. — EuYu, Nov 05 '12 at 03:47
@Andy I suggest that you tell us in which context your professor told you all this. For this problem, I suggest that you gives us all the strings of length $\le 10$ that you could not find. — Phira, Nov 05 '12 at 10:00

score 2 · Answer 1 · answered Nov 05 '12 at 00:44

2

(The following was shown to me a few years ago by David Kelly, who used this discovery to generate an approximation of the Sierpinski Triangle by looking at Pascal's Triangle in base 2 -- though the details of this part escape me.)

Let $n \in \mathbb{N}$, and let:

$$F(n) = \textrm{max}\{k \in \mathbb{N} \, \colon \, 2^k \textrm{ divides }n\}.$$

$$B(n) = \textrm{ count of 1s in the base-2 representation of } n.$$

$$P(n) = \textrm{ count of odd numbers in the } n\textrm{th row of Pascal's Triangle.}$$

Proposition: For every $n \in \mathbb{N}$, the following hold:

$F(n) + B(n) = n,$
$P(n) = 2^{B(n)}.$

answered Nov 05 '12 at 00:44

Charles Boyd

672

This seems interesting, but I am wondering how this relates to proper strings? – Andy Nov 05 '12 at 00:52
Well, the values for B(n) and P(n) are obtained by string operations. – Charles Boyd Nov 05 '12 at 00:59

Hendrik Jan · Answer 2 · 2012-11-05T01:06:00.473

1

You start by drawing a very large example of the triangle. Or finding it somewhere on the internet. Then start looking for regularities. Patterns that occur.

(edit). My initial ideas. You can see long runs of $1$'s or long runs of $0$'s. I can see $0110$, by I think I cannot find $01110$. Why? What can be above that sequence...

edited Nov 05 '12 at 01:06

answered Nov 05 '12 at 00:25

Hendrik Jan

1,970

That much I figured :) But patterns only yield so much insight.... and for me, none at all :P – Andy Nov 05 '12 at 00:27

Exploring Properties of Pascal's Triangle $\pmod 2$

2 Answers2

Linked