(It should first be stated that I'm all new to this kind of stuff, so do tell if anything turns out to be obvious to the more experienced reader, or even incorrect.)
I've been considering the following problem: let $f_n $ be a sequence of real-valued functions defined over some subset of the reals, which satisfy the initial condition $f_0(x) = q(x)$ and the following recurrence relation for all relevant $x$:
$$f_{n+1}(x) = q(x) + \frac{p(x)}{f_n(x)} \tag{1}$$
where $q$ and $p$ are polynomials which we'll require to be linear, for now.
Limiting functions and the non-critical region. The obvious question is whether the sequence has a limiting function $f$, and what that function would be. Without caring much about the details, one could multiply both sides of $(1)$ by $f_n(x)$ and take the limit as $n$ approaches infinity to get, for the same relevant $x$, the following relation: $$f^2(x) - q(x)f(x) - p(x) = 0 \tag{2}$$ Using the quadratic formula, we identify two possible candidates for a limiting function:
$$f_\pm(x) = \frac{q(x) \pm \sqrt{q^2(x) + 4p(x)}}{2} \tag{3}$$
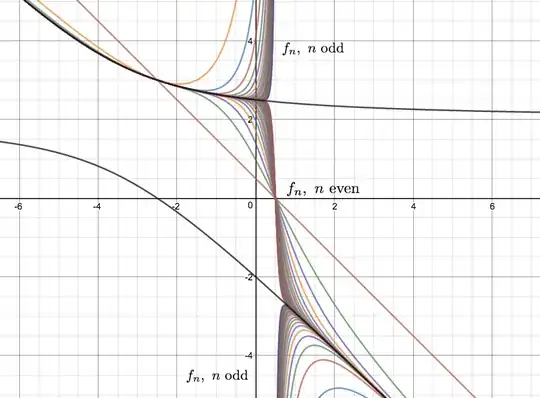
which of course makes sense as long as $\delta(x) \doteq q^2(x) + 4p(x) \geq 0$. I have confirmed it graphically that, indeed, in the non-critical region ($\delta > 0$), the $f_n$'s do tend to cluster around one of the $f_\pm$'s; they will switch to the other one at all solutions of $q$ (and this fact holds generally, even for non-polynomial $p$ and $q$!).
Actually, at the points where $q$ vanishes we see that all $f_n$ with even $n$ must vanish too, while all $f_n$ with odd $n$ must careen off to infinity and come back from the other side, before both families approach the other limiting function. I am led to conjecture that the overall limiting function should in general be undefined and have no limit at all points where $q$ vanishes, as long as those points lie within the non-critical region. An example is shown below.
The critical region and node pillars. Now, the more interesting part is the critical set (all $x$ such that $\delta(x) \leq 0$). In this region, there is no limiting function to converge to and the $f_n$'s are free to do what they want. However, a curious, seemingly regular behavior seems to arise.
Consider, for example, the case in which $p(x) = -x$ and $q(x) = x$. Then the critical set is the interval $[0,4]$. Here is a picture of the mayhem that happens with the first $50$ functions in the sequence in this interval.
You can clearly discern the "node pillars" clearing up the mess at occasional points; for example, we see two vertically aligned nodes at $x = 1$, three nodes at $x = 2$, four nodes at $x \approx 2.618$ (yes, the square of the golden ratio $\phi$), five nodes at $x = 4$, six nodes at $x \approx 3.247$ (yes, the silver constant $S$), and so on until the end of the critical interval is reached. After a bit of research, I found that these numbers are known as Beraha constants
$$B_n = 2 + 2\cos\left(\frac{2\pi}{n}\right) = 4\cos^2\left(\frac{\pi}{n}\right) \tag{4}$$
These constants seem to connect different areas of mathematics together: the golden ratio $B_5$ of course pops up everywhere, the silver constant $B_7$ comes up in the 3-cycle of the logistic map in chaos theory, $B_9$ is related to the bond percolation threshold of the honeycomb graph in percolation theory, and so on.
The nature of node pillars. But the more curious part comes when one inspects which functions are generating each node pillar. We find that if a node pillar contains $k - 1$ nodes (pillar of order $k$), then for each node there exists a unique $m\ \ \mathrm{s.t.}\ \ 0 \leq m < k$ such that, for all $f_n$ passing through that node,
$$n \equiv m \pmod k \tag{5}$$
and all the $k-1$ possibilities for such $m$'s are exhausted within each pillar. Let us call the node associated with $m$ the $m$th node of order $k$, and the node for which $m = k$ the leading node.
So, for example, at $x = B_5 = \phi^2 \approx 2.618$ we have $4$ nodes, one (the leading node) generated by $f_0, f_5, f_{10}, \dots$, the one below generated by $f_1, f_6, f_{11}, \dots$, the one even lower generated by $f_2, f_7, f_{12}, \dots$, and the lowermost one generated by $f_3, f_8, f_{13}, \dots$, while all other functions ($f_4, f_9, f_{14}, \dots$) have a vertical asymptote.
(It is noteworthy that an identical behavior also happens at $x = \phi^{-2} \approx 0.382$!)
The fact that there are places where some of the functions in our sequence vanish and some blow up to infinity does resemble the behavior we found in the non-critical region at the zeros of $q$, except here we have more than these two options ($k-1$ of them for a pillar of order $k$). Could it be perhaps that pillars of order $2$ are located at the zeros of $q$ outside of the critical interval?
EDIT: Surprisingly, after some careful search in the OEIS, I was able to find a family of polynomials of degree $\ell$ that vanish exactly where a pillar of order $2\ell + 1$ occurs. These polynomials are given by the formula
$$\chi_{2\ell + 1} (x)= \sum_{j=0}^\ell (-1)^j \binom{2\ell - j}{j}x^{\ell - j} \tag{6}$$
and are important in graph theory – they are the chromatic polynomials of maximal planar graphs. I've also found they vanish at the generalized Beraha constants (my own name):
$$\chi_{2\ell + 1}(x) = \prod_{k=1}^\ell \left(x - 4\cos^2\left(\frac{\pi k}{2\ell + 1}\right)\right) \tag{7}$$
I wonder what the polynomials $\chi_{2\ell}$ vanishing at the even-order pillars might look like, and whether there can be a common formula that holds for all $\ell$.
Height of nodes. As for the height of each node, that's a whole different story. Here are the node heights registered for the main pillar orders (arranged for increasing $m$): $$ \begin{split} k=3 &\quad y = 1;\ 0;\ \infty. \\ k=4 &\quad y = 2;\ 1;\ 0;\ \infty. \\ k=5 &\quad y = \phi^2;\ \phi;\ 1;\ 0;\ \infty. \\ k=6 &\quad y = 3;\ 2;\ 1.5;\ 1;\ 0;\ \infty. \\ k=7 &\quad y = B_7;\ B_7 - 1;\ \frac{B_7 - 1}{B_7 - 2};\ \frac{B_7}{B_k - 1};\ 1;\ 0;\ \infty. \\ k=8 &\quad y = B_8;\ B_8 - 1;\ \frac{B_8 - 1}{B_8 - 2};\ \frac{1}{B_8 - 3};\ \frac{B_8}{B_8 - 1};\ 1;\ 0;\ \infty. \\ k=9 &\quad y = B_9;\ B_9 - 1;\ \frac{B_9 - 1}{B_9 - 2};\ \frac{1}{B_9 - 3};\ \frac{1}{4 - B_9};\ \frac{B_9}{B_9 - 1};\ 1;\ 0;\ \infty. \\ \end{split}$$ The pattern is not completely clear, for now. Nonetheless, a beautiful property seems to emerge: whichever $k$ we pick, the $m$th element in the respective sequence is related to the associated Beraha constant (the height of the leading node) through the very same "rational" relationship, i.e., they can be expressed as a rational function of $B_k$ that does not depend directly on $k$; ever more interestingly, the same seems to hold for the $(k - m)$th element. So, for example,
$$\begin{split} \beta_{k;0} &= B_k \\ \beta_{k;1} &= B_k - 1 \\ \beta_{k;(k-4)} &= \frac{B_k}{B_k - 1} \end{split}$$
where we indicate with $\beta_{k;m}$ the $m$th element in the $k$th sequence.
The overlapping of such properties does not seem to be a problem! Take, e.g., $k = 4$: we have that $k - 4 = 0$, so both the first and the third rational expressions written above should be satisfied for $\beta_{4;0}$. This is indeed the case: $$\beta_{4;0} = B_4 = \frac{B_4}{B_4 - 1}$$ so that $$B_4(B_4 - 1) = B_4 \Rightarrow B_4^2 - 2B_4 = 0 \Rightarrow B_4 = \pm 2 $$ which is true, since $B_4 = 2$. The same holds for $k = 5$, where we have $$\beta_{5;1} = B_5 - 1 = \frac{B_5}{B_5 - 1} $$ so that $$(B_5 - 1)^2 = B_5 \Rightarrow B_5 = \frac{3 \pm \sqrt{5}}{2} = \begin{cases} 0.381966,\ \mathrm{or} \\ 2.618033 \end{cases} $$ of which the second is true. (Notice how $\phi^{-2}$ comes back through the window!)
Thus, there seems to be a way to identify (seemingly linear) rational expressions in $B_k$ alone for $\beta_{k;m}$ and $\beta_{k;(k-m)}$ that hold $\forall k$. Call the first kind forward expressions and the latter kind backward expressions. As we've seen, it actually seems that the overlap between a forward and a backward expression (and which ones do overlap depends of course on $k$) is what dictates the value of $B_k$.
Lastly, if we look at $k = 5$, we notice that $\beta_{5;1}^2 = \beta_{5;0}$. One might conjecture that some kind of irrational pattern lurks behind the $\beta$ sequences; and indeed, it seems correct, but only for odd $k$. The relationship is the following:
$$\beta_{(2k+3);0} = \beta_{(2k+3);k}^2$$
So my questions are,
- Why do the functions in our sequence need to switch which of the $f_\pm$ they are approximating when $q$ has a zero? How do they choose which one to start with? And why do the $f_n$'s there have to behave as they do for even and odd values of $n$?
Why do the node pillars distribute according to the Beraha constants in our specific example?What truths does this motivation entail in the general case?Why do node pillars of order $k$ seem to recur for values of $x$ other than $B_k$ (as mentioned above in the case of $k = 5$)? How are these values of $x$ related to $B_k$?- EDIT – struck-through questions have now become: Why do the odd-order pillars occur at the zeros of the chromatic polynomials $\chi_{2\ell + 1}$? Do there exist similar polynomials for even-order pillars?
- Why do the nodes distribute within pillars according to the modular equivalence $(5)$ above? How can we explain the backward and forward patterns in their height in the general case?
 $1/2$.">
$1/2$.">