Does symmetry in Hamiltonian function implies symmetry in the Hamiltonian flow?

Question

OK, this is probably an elementary question, but I still cannot figure it out.

I have a Hamiltonian function on $\mathbb{R}^2$ that is even in the second argument, i.e. $H(x,-y) = H(x,y)$.

Then we get the Hamiltonian vector field $$X_H(x,y) = (H_y(x,y),-H_x(x,y)).$$

It holds that $H_x(x,-y) = H_x(x,y)$ and $ H_y(x,-y) = - H_y(x,y) $.

I am interested in the properties of the Hamiltonian flow, i.e. $$\dot{\psi}(t) = X_H \circ \psi(t).$$

Are the above enough to show that we can always choose initial conditions such that if $$\psi(t) = (\psi_x(t),\psi_y(t))$$ then $\psi_x(-t) = \psi_x(t)$ and $\psi_y(-t) = -\psi_y(t) $?

Answer 1

It's pretty easy to show that if your Hamiltonian has these properties, then the system posesses the following property: if $(x(t), y(t))$ is a solution, then $(x(-t), -y(-t))$ is a solution too (this system is reversible with involution $(x, y) \mapsto (x, -y)$). Reusing my illustration from this answer and forgetting that I've used $(u, v)$ axes instead of $(x, y)$ [and also confused $u$ with $v$ on my illustration], we can get the idea where we should place the initial conditions:

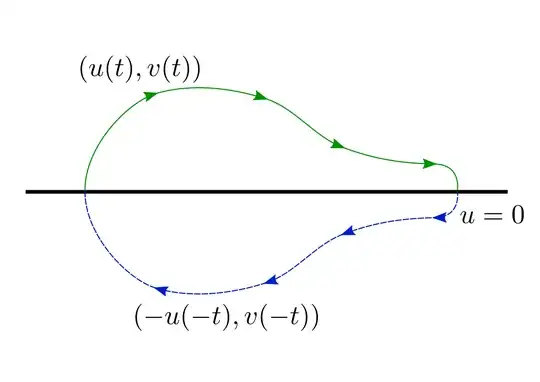
Well, the answer is: put it on $y = 0$, which is the line of fixed points of this involution. You could also get this from substituting $t=0$ in your "equation" of interest: it would gave you a condition that $\psi_y (0) = -\psi_y(0)$ thus $\psi_y (0) = 0$.

ADDED LATER

The final step requires us to prove that if we take a trajectory with $(x(0), y(0)) = (x^\ast, 0)$ then $(x(t), y(t)) = (x(-t), -y(-t))$. If we allowed to use some theorems, then it is known that reversible flow $\phi^t$ is conjugated with its inverse using the involution $h$: $$ \phi^t \circ h = h \circ \phi^{-t}.$$

Since $h(x^\ast, 0) = (x^\ast , 0)$ we straightforwardly get that for such initial conditions holds $(x(t), y(t)) \equiv (x(-t), -y(-t))$.

But right now I don't remember how to prove this statement about conjugacy :)

Well, it's funny that Meiss' book uses this conjugace property as the definition from the get go and Wiggins' book doesn't speak about this at all. It required some time to figure out the proof, but it turned to be pretty simple. So we have a flow $\phi^t$ generated by a system of ODEs. Then $\phi^t(z)$ is a solution that passes through point $z$ at $t=0$ (becase $\phi^0 = {\rm id}$). From reversibility we also know that if $\phi^t(z)$ is a solution, then $h \circ \phi^{-t}(z)$ is a solution too. Let's consider a point $x$ and a point $y = h(x)$. Trajectories $\phi^t(x)$ and $\phi^t(y)$ pass through these points respectively. Also, we know that $h \circ \phi^{-t}(y)$ is a trajectory too. But here's the funny thing that happens: both $\phi^{t}(x)$ and $h \circ \phi^{-t}(y) = h \circ \phi^{-t} (h(x))$ pass through the same point $x$ at $t = 0$. Because of flow properties these must be the same trajectories, i.e. $\forall t \; \phi^{t}(x) = h \circ \phi^{-t}(h(x))$. But the point $x$ is arbitrary, hence $\phi^t = h \circ \phi^{-t} \circ h$.