Formal proof of Lyapunov stability

Question

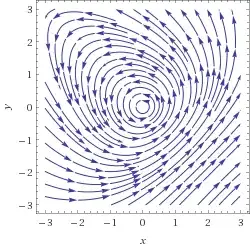
I was trying to solve the question of AeT. on the (local) Lyapunov stability of the origin (non-hyperbolic equilibrium) for the dynamical system $$\dot{x}=-4y+x^2,\\\dot{y}=4x+y^2.\tag{1}$$

The streamplot below indicates that this actually is true.

Performing the change of variables to polar coordinates $x=r\cos\phi$, $y=r\sin\phi$ and after some trigonometric manipulations we result in $$\dot{r}=r^2(\cos^3\phi+\sin^3\phi)\\ \dot{\phi}=4+r\cos \phi \sin\phi(\cos \phi -\sin \phi )$$

From this set of equations I want to prove that if we start with sufficiently small $r$ then $r$ will remain bounded with very small variations over time.

My intuitive approach: For very small $r$ $$\dot{\phi}\approx 4$$ that yields $$\phi(t)\approx 4t +\phi_0$$ If we replace in the $r$ dynamics we obtain $$\dot{r}\approx r^2\left[\cos^3(4t+\phi_0)+\sin^3(4t+\phi_0)\right]$$ Integrating over $[0,t]$ we obtain $$\frac{1}{r_0}-\frac{1}{r(t)}\approx \int_0^t{\left[\cos^3(4s+\phi_0)+\sin^3(4s+\phi_0)\right]ds}$$ The right hand side is a bounded function of time with absolute value bounded by $4\pi$ since $$\int_{t_0}^{t_0+2\pi}{\left[\cos^3(4s+\phi_0)+\sin^3(4s+\phi_0)\right]ds}=0 \quad \forall t_0$$ Thus for very small $r_0$ it holds true that $r(t)\approx r_0$.

I understand that the above analysis is at least incomplete (if not erroneous) and I would be glad if someone can provide a rigorous treatment on the problem.

I think that a "singular-perturbation like" approach may be the solution (bounding $r$ by $\epsilon$) and considering the comparison system to prove the global boundedness result but I haven't progressed much up to now.

Answer 1

There is another insight that could be given by streamplot. Two observations: 1) trajectories are suspiciously symmetric; 2) most of them look like closed trajectories. Therefore, it's not reasonable trying to find only Lyapunov function: Lyapunov function means some sort of dissipation near equilibrium, and here it looks more like that we have a family of closed trajectories around equilibrium point, i.e. some sort of conservation. To prove that we have closed trajectories we might use two concepts: first integral and equivariant system (system with symmetry). Both methods can help proving that some integral curves are closed: first integral method utilizes the fact that integral curves lie on its level sets (and if some of them closed and don't contain equilibria, then integral curve is closed); equivariance in its simplest form utilizes symmetries like reflection.

I tried to come up with first integral for this system, but I was unsuccessful. Then I decided to check the symmetry. I expected that symmetry will be generated by reflection w.r.t. line $y=-x$ and I wanted to check that. First, let's make the change of variables: $$ u = x + y, \; v = x - y .$$ The system of ODEs for new variables looks like this: $$ \dot{u} = 4v + \frac{u^2+v^2}{2}, $$ $$ \dot{v} = u (v - 4). $$

I had a suspicion that mapping $(u, v) \mapsto (-u, v)$ sends trajectories to trajectories. Let's check this. Suppose we have solution $(\hat{u}(t), \hat{v}(t))$; will $(-\hat{u}(t), \hat{v}(t))$ be the solution too?

$$ \frac{d}{dt} \left ( -\hat{u}(t) \right )= -\frac{d}{dt} \left (\hat{u}(t) \right ) = - 4\hat{v}(t) - \frac{\hat{u}^2(t)+\hat{v}(t)^2}{2} \neq 4\hat{v}(t) + \frac{(-\hat{u}(t))^2+\hat{v}(t)^2}{2} $$ $$ \frac{d}{dt} \left ( \hat{v}(t) \right ) = \hat{u}(t) (\hat{v}(t) - 4) \neq (-\hat{u}(t) )\cdot(\hat{v}(t) - 4) . $$

Well, this simply means that $(u, v) \mapsto (-u, v)$ isn't a symmetry of this system of ODEs. Euh. There's an annoying minus sign that spoils everything. Nor $(u, v) \mapsto (-u, -v)$, nor $(u, v) \mapsto (u, -v)$ won't fix it. At this moment I've remembered that there are also reversible systems. This suggests me to check whether mapping $(\hat{u}(t), \hat{v}(t)) \mapsto (-\hat{u}(-t), \hat{v}(-t)$ sends trajectories to trajectories. And yeah, it sends :)

What all this fuss was about? Why reversibility (the property, that $(-u(-t), v(-t))$ is also a solution when $(u(t), v(t))$ is a solution) helps here? Let me illustrate this:

I think that image is pretty self-explanatory. From here follows that all trajectories that intersect $u=0$ twice are closed. It's not hard to show that trajectories in some neighbourhood of origin have this property. From this we conclude that origin is center equilibrium, which is Lyapunov stable but not asymptotically Lyapunov stable.

Answer 2

1. OP's streamplot suggests that the line $y=x-4$ is a flow trajectory. If we insert the line $y=x-4$ in OP's eq. (1) we easily confirm that this is indeed the case.

2. From now on we will assume that $y\neq x-4$. It is straightforward to check that the function $$H(x,y)~:=~\frac{xy+16}{x-y-4}-4 \ln |x-y-4| $$ is a first integral/an integral of motion: $\dot{H}=0$.

3. In fact, if we introduce the (non-canonical) Poisson bracket $$B~:=~\{x,y\}~:=~ (x-y-4)^2 ,$$ then OP's eq. (1) becomes Hamilton's equations $$ \dot{x}~=~\{x,H\}, \qquad \dot{y}~=~\{y,H\}. $$

4. The above result was found by following the playbook laid out in my Phys.SE answer here: $B$ is an integrating factor for the existence of the Hamiltonian $H$.