2

Let $p \in \mathbb {c} $ be a period point of a rational function $R$ i.e. it is a fixed point for an Iterate $R^n $. If $(R^n)'(p)=e^{2\pi i t} $ for some $t \in \mathbb {Q} $ then p is called rational indifferent. For a minimal $n $, $(p,R(p),R^2 (p),...,R^{n-1}(p))$ is then called rational indifferent cycle.( Are my assumption true?) Now I am looking for some examples of them, preferably cycles with order $>1$. Since I already found $R(z)=e^{2 \pi i t }(z+z^2) $ which has a rational indifferent fixpoint in the origin. Thanks for your help.

deavor
  • 997

2 Answers2

3

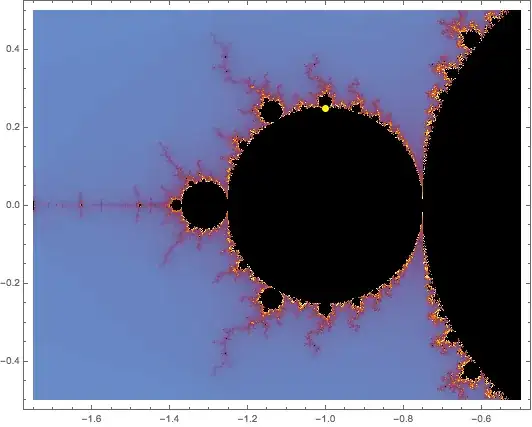
Let $t\in\Bbb Q$, $t\ne0,1$ and $$ R_t(z)=z^2+\frac14\,e^{2\pi it}-1. $$ Then $$ p_\pm=\frac{1}{2} \left(-1\pm\sqrt{1-e^{2 i \pi t}}\right) $$ are periodic of period $2$ and $(R^{(2)})'(p_\pm)=e^{2 i \pi t}$.

Note that these points $t = \frac14\,e^{2\pi it}-1$ all lie on the circle of radius $1/4$ centered at the point $c=-1$. This is exactly the boundary of the period 2 disk in the Mandelbrot set. If, for example, we set $t=3/4$, we obtain $z^2-1+i/4$ as shown in yellow below:

enter image description here

More generally, the rational values of $t$ produce points where a smaller bulb is attached. The Julia set for this value of $c$ looks like so:

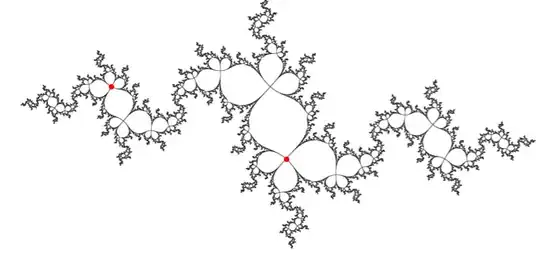
enter image description here

The red dots form an orbit of period 2.

Julián Aguirre
  • 77,704
  • 1
    Thank you for your answer. Is there maybe a similary simple example for $deg R>1$. I am especially asking in regard to the theorem that all these rationally indifferent cycles are in the Julia Set – deavor May 08 '17 at 14:32
  • I have included examples of degree $2$ in the answer. – Julián Aguirre May 08 '17 at 16:08
  • https://commons.wikimedia.org/wiki/File:Parabolic_Julia_set_from_period_2_thru_internal_angle_1_over_4.png – Adam May 09 '17 at 20:21
  • @Julián Aguirre: Is it t = 1/4 not 3/4 ? – Adam Jun 17 '21 at 18:13
2

you can use program Mandel for it:

  • choose your function
  • on the parameter plane click inside component
  • choose t ( = internal angle = rotation number) : Menu/Points/bifurcation
  • then go to dynamic plane
  • choose periodic point ( it is what you are looking for)

See also parabolic Julia sets:

HTH

Adam
  • 1,776