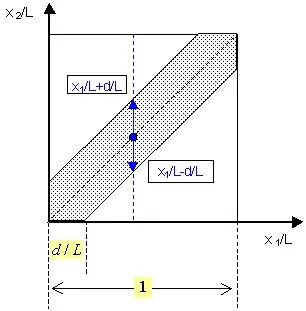
Suppose there is a line with fixed length $L$, and $x$ is the position of the points on this line ranging from $0$ to $L$, i.e. $0 \leq x \leq L$, then what is the probability distribution of fitting two circles with diameter $d$ ($d$ is always less than half of the length, $d < L / 2$). The first circle can be randomly positioned any point (including both ends), the centre of the first circle, $x_1$, can have values $0$, $L$ and any value between them. but the second circle, with its centre at $x_2$, cannot overlap - only it can be adjacent, so always $\vert x_1-x_2 \vert \geq d$.
How can I find a generic statement for the probability of distribution of these two circles?
$x$ is the variable for the $1$-dimensional coordination of circles centres.
For example, assuming $L=1$, and $d=0.2$, if the $x$ for the first circle happens to be at $x=0.1$, the second circle can be located at any point between $x=0.2$ and $x=1$ (to avoid overlapping), so $80\%$ of $L$. if $x_1$ ($x$ for 1st circle's centre)$=0.2$, the $x_2$ can have only $70\%$, but if $x_1=0.4$, $x_2$ has again $80\%$ chance.
I'm looking for a probability model to describe this problem in general in terms of $L$ and $d$.