3

I am sorry if this question sounds stupid, but I have this doubt in mind ever since I was a child.

We know ellipses are symmetrical figures, having 2 axes of symmetry.

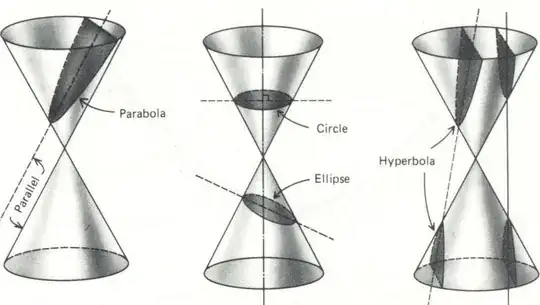
We know that an ellipse is generated from a cone when a plane cuts it at some angle say $\theta$ ( see conic section) Now the cone is not same shape at both ends (my doubt), so a perfect ellipse shouldn't be formed from cone as it would result in a distorted ellipse with only one axis of symmetry (my thinking)

I think that an ellipse that is a cylindric section is seemingly more symmetrical than the ellipse that is a conic section

How can I be satisfied that conic section ellipse is truly an ellipse? I think we need to solve the cone with a plane equation right?

Also, How can both cone and cylinder generate perfect ellipse?

enter image description here

Here in this figure, to me the ellipse looks imperfect. But really it isn't!

EDIT

Recently (August 1, 2018) a new video was added by 3B1B adressing this very question, and he used dandelin sphere proof to show equivalence of Thumbtack construction and slicing cone/ cylinder construction. Watch here: Youtube

jonsno
  • 7,671
  • The axes of symmetry of the ellipse are not necessarily the axes of symmetry of the cone. Think about a conic section with angle almost $90$ degrees to the base. – uniquesolution Apr 03 '17 at 08:09
  • @uniquesolution Yes I get what you say, but I find it rather hard to believe. How can both cone and cylinder generate perfect ellipse? – jonsno Apr 03 '17 at 08:11
  • 1
    You see, beliefs and "how-can" questions are really hard to settle. – uniquesolution Apr 03 '17 at 08:12
  • @uniquesolution An ellipse, as tought in class was locus of P such that its distance from Focus S was less than its distance from directrix M. How can we be sure that this conic section is ellipse? – jonsno Apr 03 '17 at 08:14
  • 2
    That's a very old question that has some very old answers, don't you think? – uniquesolution Apr 03 '17 at 08:16
  • 1
    May be this helps :https://en.wikipedia.org/wiki/Dandelin_spheres – Jaideep Khare Apr 03 '17 at 08:20
  • @samjoe But did you not observe or realize at end of minor axis the focus/ directrix combination $(F1,D1) $ that you were so far talking about suddenly switched to$(F2,D2) ?$ And also that either combination is equally holding good? – Narasimham Apr 03 '17 at 08:23
  • 1
    That figure doesn't depict the ellipse of intersection: it depicts a projection onto the surface of your monitor. And the projection, incidentally, looks like a perfect ellipse to my eye. –  Apr 03 '17 at 10:26
  • I was trying to figure out what OP meant by distance from focus < distance to directrix M in the intersection plane. – Narasimham Apr 03 '17 at 10:36

1 Answers1

1

Short answer:

The intersection of a plane and a quadric (among which cones and cylindres) is a conic, described by a quadratic equation $$ax^2+by^2+2cxy+2dx+2ey+f=0.$$

The conics are 4-way symmetrical curves. This is proven by the fact that the equation can be reduced to the form

$$\lambda x^2+\mu y^2=\nu$$ by translation and rotation (except in a few degenerate cases).

In polar coordinates, a conic can be represented by the equation

$$r=\frac l{1+e\cos\theta}.$$

By evenness of the cosine function, you expect the curve to by symmetrical around the axis $y=0$. But there is another, unexpected, symmetry. Indeed, we can rewrite

$$r^2=(l-er\cos\theta)^2$$ or in Cartesian coordinates

$$x^2+y^2=l^2-2ex+e^2x^2$$ then by completing the square

$$(1-e^2)\left(x+\frac{e}{1-e^2}\right)^2+y^2=l^2+\frac{e^2}{1-e^2}.$$

So the other symmetry axis is $$x=-\frac e{1-e^2}.$$

enter image description here

Again, this is due to the degree of the algebraic equation.

  • 1
    Admittedly, this doesn't help geometric intuition a lot. –  Apr 03 '17 at 08:31
  • Thanks a lot for your answer. It explains a lot, but I am currently trying to find a procedure to convert a second degree expression like one you described into the reduced form as you mentioned, like in a question I asked some time back here. I also don't know from where the $\Delta$ came into play, and if you have knowledge on the method of factoring by rotation and translation, please do share! Thank you! – jonsno Apr 03 '17 at 10:46
  • @samjoe: maybe this: http://math.stackexchange.com/a/1769439/65203 –  Apr 03 '17 at 10:51
  • Thanks that does help alot. I can handle translation, but rotation is difficult for me, i can identify a standard curve, but not any general curve, but your answer helped a lot. – jonsno Apr 03 '17 at 11:53
  • There were some attempts to address the geometric intuition here: http://math.stackexchange.com/questions/2184505/why-ellipse-is-a-conic-section – David K Apr 03 '17 at 13:12
  • A video by 3B1B adressing similar question: https://www.youtube.com/watch?v=pQa_tWZmlGs – jonsno Aug 24 '18 at 14:48