Calculus of variations with two functions and inequality

Question

I wish to extremise

$$ Q = \int_0^h u \, \,dy $$

with the following constraints

$$B = \int_0^h u g \, \, dy \\ M = \int_0^h u^2 +\left(\int_0^y g \, \,dy^*\right) \, \, dy$$

where $M,B$ are constant. So my idea is to set this up as a variational problem as such

$$\varepsilon \left(Q + \lambda B + \mu M\right) = 0$$

We assume

$$u = u_0 + \varepsilon u_1 \\ g = g_0 + \varepsilon g_1 $$

I also wish to constrain that $0 < g \leq g^*$ for some given $g^*$, but I will ignore that for the time being. Taking $O(\varepsilon)$ terms gives

$$\varepsilon \left[\int_0^h u_1 + \lambda(u_0g_1+u_1g_0) + \mu 2 u_0u_1 + \mu\left[y \int_0^h g_1 \right]_0^h - \mu \int_0^h y g_1 \, \,dy \right] = 0$$

Where I have used integration by parts on the $\int g$ term in $M$. This gives

$$ \int_0^h \left[ u_1(1 + \lambda g_0 + 2 \mu u_0) + g_1(\lambda u_0 + \mu(h-y) \right] = 0 $$

Taking the two terms to be independent gives

$$u_0 = -\frac{\mu}{\lambda}(h-y) \\ g_0 = -\frac{1}{\lambda} + 2\left(\frac{\mu}{\lambda}\right)^2(h-y)$$

All good so far I think? I expected $u_0,g_0$ to be linear. For ease of notation set $\omega = -\mu / \lambda$ and $-1/\lambda = \beta$.

Then we can arrive substituiting $u_0, g_0$ into the definitions of $M,B$ with some algebra, at

$$M = \omega^2 h^3 + \frac{\beta h^2}{2} \\ B = \frac{2}{3}\omega^3 h^3 + \frac{\beta \omega h^2}{2}$$

And hence, these two simultaneous equations give

$$Q = \frac{(3(M \omega - B)^{2/3}}{2 \omega} $$

So here is where I run out of steam a bit. I guess I want to extremise $Q$ so take

$$\frac{\partial Q}{\partial \omega} = 0 \Rightarrow \omega = \frac{3B}{M}$$

However, this $\omega$ implies that $\beta = -2M / h^2 < 0$, which means that the constant term in $g_0$ is negative, which is unphysical in my set up, so we must have $\beta = 0$ at the maximal value.

Proceeding with $\beta = 0$ gives us

$$\omega = \frac{3B}{2M}$$

which gives me a maximal

$$Q = \frac{M}{2^{2/3} 3^{1/3} B^{1/3}}$$.

However, I am not sure if this answer/my method is correct, nor how to incorporate the inequality constraint that $g_0$ is smaller than some fixed value.

I can get a measurement for maximal $Q$ via a different method, which provides me with the correct powers/dimension, but the prefactors (in particular the $2^{2/3}$) are incorrect.

Any pointers on how to answer this type of question? How to incorporate the inequality? Or if indeed my method is correct.

EDIT

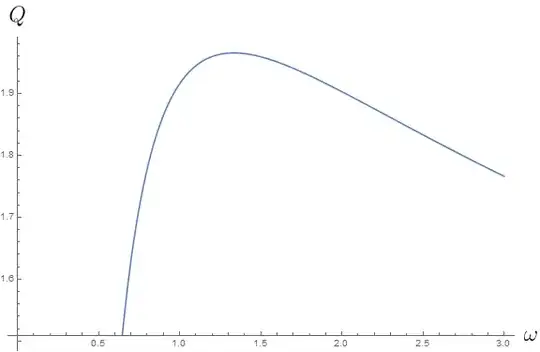
To show why I select $\beta = 0$ as the maximal case. Consider the plot of $Q$ against $\omega$. If we input some reasonable (physically sound) values for $M = 4.5$ and $B = 2$ we have

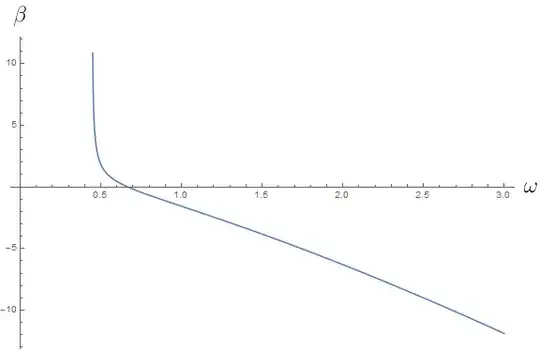
So we can see that $Q$ has a maximal value. However, plotting $\beta$ against $\omega$ for the same values of $M,B$ shows us that $\beta$ gives a negative value at this maximal value, which is unphsyical. So the maximal $Q$ goes with $\beta = 0$.

Answer 1

The proposed problem is typical for problems of the calculus of variations. A classical (exact) approach to solving similar problems requires us to present the integrand as a function of an independent variable, an optimized function, and its derivative. Abandonment of the use of the derivative allows us to consider the author's solution as a kind of trial and error method.

To use the classical approach, one can use the function $$G(y) = \int\limits_0^yg(y^*)dy^*,\qquad(1)$$ then $$\begin{cases} g(y) = G'(y)\\ Q(u) = \int\limits_0^h q(u)\,dy,\quad q(u) = u\\ B(u,G') = \int\limits_0^h b(u,G')\,dy,\quad b(u,G') = uG'\\ M(u,G) = \int\limits_0^h m(u,G)\,dy,\quad m(u,G) = u^2+G. \end{cases}\qquad(2)$$ Let us try to combine the elements of Lagrange multipliers method with theory of the Euler-Lagrange calculus of variations.

Lagrange function is $$F(u,G,\lambda,\mu) = Q + \lambda(B-B_0) + \mu(M-M_0),$$ the variations are $$\begin{cases} \dfrac{\delta q}{\delta u} = 1\\ \dfrac{\delta b}{\delta u} = G' = g\\ \dfrac{\delta b}{\delta G} = -\frac d{dy}u = -u'\\ \dfrac{\delta m}{\delta u} = 2u\\ \dfrac{\delta m}{\delta G} = 1, \end{cases}\qquad(3)$$ where have used Euler-Lagrange theorem of variations $$\dfrac{\delta F(y,f,f')}{\delta f} = F'_f - \dfrac{d}{dy}F'_{f'}$$ Equaling to zero $\dfrac{\delta F}{\delta u},\ \dfrac{\delta F}{\delta G},\ F'_\lambda,\ F'_\mu,\ $ one can get the system $$\begin{cases} 1+\lambda g + 2\mu u = 0\\ -\lambda u' + \mu = 0\\ \int\limits_0^hug\,dy = B_0\\ \int\limits_0^h(u^2 +G)\,dy = M_0. \end{cases}\qquad(4)$$ The second equation means $$\boxed{u = \frac{\mu}{\lambda}\,y+u_0},$$ then $$Q = \int\limits_0^h \left(\frac{\mu}{\lambda}\,y+u_0\right)\,dy = \frac{\mu }{2\lambda}h^2+u_0h,\qquad(5)$$

Parameters $B_0$ and $M_0$ can be used for calculation of unknowns $\lambda $ and $\mu$ from the system $(4).$

$$\begin{cases} g(y) = -2\frac\mu\lambda \left(\frac{\mu}{\lambda}\,y+u_0\right) - \frac1{\lambda},\\ G(y) = u_0^2-\left(\frac{\mu}{\lambda}\,y+u_0\right)^2 - \frac1{\lambda}y,\\ B_0 = \frac23\left(u_0^3 - \left(\frac{\mu}{\lambda}\,h+u_0\right)^3\right) + \frac1{2\mu}\left(u_0^2 - \left(\frac{\mu}{\lambda}\,h+u_0\right)^2\right),\\ M_0 = u_0^2h-\frac1{2\lambda}h^2, \end{cases}$$ $$\begin{cases} 4\left(\frac{\mu h}\lambda\right)^3 + 12u_0\left(\frac{\mu h}\lambda\right)^2 + 3\left(4u_0^2+\frac h\lambda\right)\left(\frac{\mu h}\lambda\right) +6u_0\frac h\lambda + 6B_0 = 0\\ \frac h\lambda = 2u_0^2 - 2\frac {M_0}h, \end{cases}$$ $$\left(\dfrac{\mu h}\lambda\right)^3 + 3u_0\left(\dfrac{\mu h}\lambda\right)^2 + \dfrac32\left(3u_0^2 - \dfrac {M_0}h\right)\left(\dfrac{\mu h}\lambda\right) + 3u_0\left(u_0^2 - \dfrac{M_0}h\right) + \dfrac32B_0 = 0$$ $$\left(\dfrac{\mu h}\lambda+u_0\right)^3 + \dfrac32\left(u_0^2 - \dfrac{M_0}h\right)\left(\dfrac{\mu h}\lambda + u_0\right) + \dfrac12\left(3B_0 - 3\dfrac {M_0}h u_0+u_0^3\right) = 0.\qquad(6)$$ The equation $(6)$ allows to obtain explicit expression for $\dfrac{\mu h}\lambda$ via $u_0$ - eg, using Vieta's substitution.

It's substitution in $(5)$ gives the requred function $Q(u_0)$.

UPD

Let us change the "fresh" conditions: $$ \begin{cases} \lambda>0\\ \mu\lambda<0\\ g(0)<g^* \end{cases}\rightarrow \begin{cases} u_0^2 > \dfrac{M_0}h,\\ \dfrac{\mu h}\lambda < 0\\ u_0 < \dfrac{\lambda g^* +1}{-2\mu}. \end{cases} $$ The first of them means that equation $(6)$ in the form of $$v^3+pv+q=0,$$ where $$v = \dfrac{\mu h}\lambda + u_0,\quad p = \frac32\left(u_0^2-\frac {M_0}h\right) > 0,\quad q = \dfrac12\left(3B_0 - 3\dfrac {M_0}h u_0+u_0^3\right),$$ have the single real root $$v = \sqrt[3]{-\dfrac q2+\sqrt{\dfrac{q^2}4 + \dfrac{p^3}{27}}} + \sqrt[3]{-\dfrac q2 - \sqrt{\dfrac{q^2}4 + \dfrac{p^3}{27}}},$$ аnd the reversal point of the sign of $\left(\dfrac{\mu h}\lambda\right)$ can be determined from the equation $$u_0^3 - \dfrac{M_0}h u_0 + \dfrac{B_0}2 = 0,$$ $$\dfrac23u_0p + B_0 = 0,$$ those the second condition should be performed for $u_0 > -\dfrac{3B_0}{2p}.$