Why ellipse is a "conic" section?

Question

When I was first introduced to conic sections, I was kinda surprised that the ellipse is one of them. I mean intuitively, if a cone is cut by a slant surface, one would expect that the cross-section is an egg-shaped one; since the flat circular sections become wider the more we go down.

It is still strange for me that why the cross-section of a cone and a slant surface becomes a symmetric ellipse and not an egg-shaped one. Can anyone explain this in an intuitive way? An answer with a mathematical proof would be nice, but becomes perfect has it been followed by some intuition.

Answer 1

We're quite familiar with the fact a planar section of the cylinder is an ellipse. Suppose the red line on the following image represents a plane, crossing a cylinder whose radius is $r$.

If a section was perpendicular to the axis, it would be a circle with radius $r$, hence its curvature would be $k_1=\tfrac 1r$ everywhere. For a slant section, however, we get an ellipse, and its curvature at the ends of its major axis would be (iirc) $k = k_1 / \cos(\alpha)$. Of course, thanks to the whole figure symmetry, we have the same $r$ and the same $\alpha$ at both ends, so both 'ends' of the ellipse are same shaped.

Let's look at the conic section now.

We have two curvatures at two 'ends' of the section curve: $$\begin{align} k_1 = \frac 1{r_1}\cdot\frac 1{\cos\alpha_1} \\ k_2 = \frac 1{r_2}\cdot\frac 1{\cos\alpha_2} \end{align}$$ Their ratio is $$\frac{k_1}{k_2} = \frac{r_2\cos\alpha_2}{r_1\cos\alpha_1}$$ From basic trigonometric identities $$\frac{k_1}{k_2} = \frac{r_2\cos(\pi/2-\beta_2)}{r_1\cos(\beta_1-\pi/2)} = \frac{r_2\sin\beta_2}{r_1\sin\beta_1}$$ From the triangles' similarity it follows that $$\frac{r_2}{r_1} = \frac{L_2}{L_1}$$ and from the law of sines $$\frac{\sin\beta_2}{\sin\beta_1} = \frac{L_1}{L_2}$$ hence $$\frac{k_1}{k_2} = \frac{L_2}{L_1}\,\frac{L_1}{L_2} = 1$$ — the section curve has both 'ends' of the same shape (equally 'round').

Possibly similar, may be a bit more general reasoning can be applied to each part of the section (not just to apexes), leading to a final conclusion: the whole section is symmetric, hence is not an egg-shaped oval.

Answer 2

There are two antagonist effects: on one hand the radius indeed increases when you go down, which "enlarges" the curve, and on another the angle between the generatrices and the cutting plane decreases, making the curve "longer". It turns out that these two effect exactly compensate each other by magic, to give a symmetric curve. (And by the way, the axis of symmetry of the ellipse is not on the axis of the cone.)

Maybe a convincing argument is by looking at the polar equation, which is of the form

$$r=\frac{ep}{1-e\cos\theta},$$ and has no reason to yield a symmetric curve (the pole is one of the foci).

But

$$r=ep+er\cos\theta=e(p+x),$$ and squaring $$x^2+y^2=e^2(p+x)^2$$ which is quadratic, hence symmetric.

Answer 3

I can't think of a really simple intuitive reason for the ellipse being a conic section. But once you know that the equation of a cone is quadratic in $(x,y,z)$, then its intersection with a plane (which we can take without loss of generality as given by $z=0$) will give a quadratic equation in $(x,y)$. And the only quadratic closed curve in the plane is an ellipse.

Answer 4

I will attempt to give an intuitive argument why it is possible for the intersection of the plane and cone to be an ellipse. This may make it easier to accept the more rigorous mathematical arguments that show that the intersection must be an ellipse.

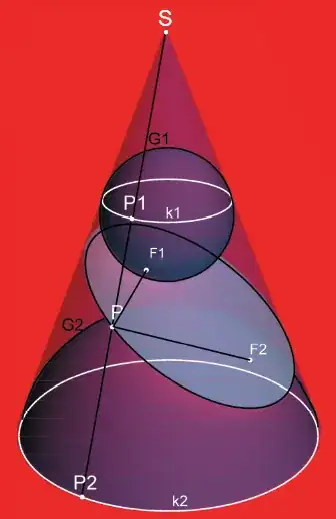
Suppose we are given a cone and a slant surface that cuts completely across the cone. Consider the many circular sections of the cone perpendicular to its axis, and the intersection of each of these circular disks with the slant surface.

Of all of these disks, the one closest to the cone's vertex intersects the slant plane at only one point. Let's call that point $P.$ The disk farthest from the cone's vertex also intersects the slant plane at only one point. Let's call that point $Q.$

The intersections of the other disks with the slant plane are line segments, and all parallel to each other and perpendicular to the line segment $PQ.$ These parallel segments can be viewed as chords or "widths" of the conic section formed by intersection of the cone and the slant plane, measured at different positions along $PQ.$

For disks very near the points $P$ or $Q,$ these line segments are short.

The largest such line segment is not between point $P$ and the axis, because as we on the slant plane from $P$ toward the axis, we are both getting closer to the axis (which would tend to increase the length of the intersection segment even if we were intersecting a cylinder instead of a cone), but we are also intersecting larger disks, which also tends to make the intersection lines longer.

Now consider the disk that intersects the axis of the cone at the same point where the slant plane intersects the axis. As the slant plane passes through this disk, the distance from the axis is having almost no effect on the length of the intersection segments (because when you take chords near the diameter of a circle, the change in the length of the chord is much, much less than the distance between the chord and the diameter), but the slant plane is still cutting into larger and larger disks, so the length of the intersection segments keeps increasing due to that effect.

Eventually, of course, the effect of moving away from the axis (cutting through smaller parts of the disk) will overcome the effect of cutting larger and larger disks, because eventually the intersection shrinks down to a point at $Q.$ So the largest intersection segment is somewhere between the axis and $Q.$

But as you will notice from a momentary examination of a cross-section of the cone along the axis, showing how the slant plane intersects the cone at points $P$ and $Q,$ the point $P$ is closer to the vertex than $Q$ is, and therefore also closer to the axis. So the midpoint of $PQ$ is somewhere between the axis and $Q.$

Now we have that the largest chord ("width") of the conic section occurs not on the axis of the cone, but somewhere between the axis and the point $Q$; and also the midpoint of $PQ$ is somewhere between the axis and the point $Q.$

It turns out these two things are in fact exactly the same distance from the axis of the cone, that is, the longest chord of the conic section passes through the midpoint of the axis $PQ$ of the conic section. This argument has not demonstrated that fact, of course; that is what the more rigorous mathematical proofs are for. But this argument should make it a little more palatable that both of these things can occur at the same place.

Answer 5

I just came across a beautiful illustration in a MO thread and recalled this question. Knowing that this question is quite old, I can't resist to add this one (it was also mentioned in the comments).

The key idea is the fact that tangents to a circle/sphere have equal length. So the only remaining part is to prove that for every cross-section not parallel to the cone's axis, such spheres exist (which is not so hard ;). Then for every $P$ on the cross-section we can write: $$|F_1P|+|F_2P|=|P_1P_2|$$

Answer 6

Intending to post this very question, I see from searching MSE that there has been discussion of it earlier this year. The following late contribution to the conversation is perhaps not as fully intuitive as the OP would like, but it does not require much thinking in three dimensions, which always stymied me before when I tried to imagine why you get symmetry on two axes, instead of an egg-shape, when slicing a cone in this way.

Take a right cone for simplicity, with vertex $V$, cut by a plane perpendicular to the plane of axial triangle $BVE$, and intersecting it in $AB$. Let $CD$, $EF$, be diameters of the circular sections cutting $AB$ at $G$ and $H$ such that $GA=HB$.

And let $GJ$, $HK$ be perpendiculars from the diameters to the circles' circumferences. Thus $GJ$ and $HK$ are also perpendiculars from the axis $AB$ of the conic section to its circumference.

Then by similar triangles $$\frac{FH}{CG}=\frac{BH}{BG}$$Likewise$$\frac{GD}{HE}=\frac{AG}{AH}$$But on the right side $BH=AG$, and $BG=AH$.

Therefore$$\frac{FH}{CG}=\frac{GD}{HE}$$Hence$$FH\times HE=CG\times GD$$

But in the circles$$CG\times GD=GJ^2$$and$$FH\times HE=HK^2$$Therefore$$GJ=HK$$Thus, in our conic section any pair of ordinates that meet the major axis at points equidistant from its vertices are equal: the section is not egg-shaped but has a minor axis about which it is also symmetrical.

If one sentence could somehow compress a brief argument into an intuition:

$AG=HB$ entails, by similar triangles, the reciprocal proportion of the circle diameter segments, hence the equality of the products of those segments and of the perpendiculars standing at their junctions.