What's a simple periodic function with a smooth curve?

Question

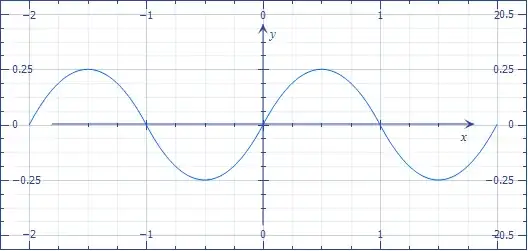
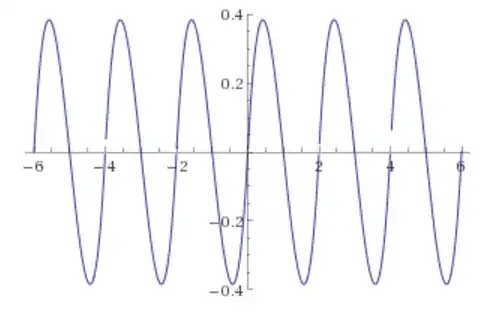
Is there a simple way to produce a smooth repetitive oscillation, using just basic arithmetic expressions, without trig functions, powers, square roots, etc.?

The numbers don't have to mean anything or approximate anything, it should just plot to something wavy.

I've spent lots of time searching but can only find things like the Taylor series, Bézier curves, etc. which are fairly complex because they're trying to calculate something in particular rather than just produce something curvy.

Thanks for your help.

score 3 · Accepted Answer · 2017-03-10T16:57:57.887

3

$$(x\bmod 1)(1-(x\bmod 1))(-1)^{\lfloor x\rfloor}.$$ You cannot spare the modulo.

Note that this is a quadratic Bezier curve.

edited Mar 10 '17 at 16:57

answered Mar 10 '17 at 16:27

Oooooops, typo. – Mar 10 '17 at 16:57
Thanks. :) Wolfram link for the curious: https://www.wolframalpha.com/input/?i=plot:+(x+mod+1)(1%E2%88%92(x+mod+1))(pow(-1,+(floor(x)))) – DenverCoder9 Mar 10 '17 at 17:01
And sine approximation... https://www.wolframalpha.com/input/?i=plot:+(4)(x%2Fpi+mod+1+)+(1%E2%88%92(x%2Fpi+mod+1))+(pow(-1,+(floor(x%2Fpi)))) – DenverCoder9 Mar 10 '17 at 22:37
Only problem is... that raising to the power of a non-integer :( – DenverCoder9 Mar 10 '17 at 22:41
1

@DenverCoder9: which noninteger ? – Mar 11 '17 at 14:57
x, as in ⌊x⌋ which the (-1) is raised by. – DenverCoder9 Mar 11 '17 at 16:07
@DenverCoder9: hem, then where is the power of a noninteger ? – Mar 11 '17 at 16:10
The -1 is being raised to the power of a non-integer. (As oppose to, say, being raised to the power of 2). – DenverCoder9 Mar 11 '17 at 16:12
@DenverCoder9: hew, what do you think the floor (which you faithfully copied) is there for ? – Mar 11 '17 at 16:14
Ah, of course slaps forehead. Sorry, not a mathematician. :) – DenverCoder9 Mar 11 '17 at 16:15

bubba · Answer 2 · 2017-03-14T00:39:47.557

3

If the floor function bothers you, you can use $$ (x\%2)*(x\%2\, - \,1)*(x\%2\, - \,2) $$ Here $x\%2$ denotes $x$ mod 2. This is a string of cubic (Bezier) curves.

edited Mar 14 '17 at 00:39

answered Mar 12 '17 at 07:37

bubba

44,617

Cool. ObWolf: https://www.wolframalpha.com/input/?i=plot:+(x+mod+2)%E2%88%97((x+mod+2)+%E2%88%92+1)%E2%88%97((x+mod+2)+%E2%88%92+2) – DenverCoder9 Mar 12 '17 at 16:12

score 1 · Answer 3 · edited Apr 13 '17 at 12:21

Chebyshev polynomials of the first kind wiggle up and down nicely. There are some pictures on the Wikipedia page.

They only require multiplication and addition.

If you want more wiggles, you can either increase the degree or string together several functions of lower degree.

If you want infinite wiggles that go on forever, you can construct periodic versions of the Chebyshev polynomials by using the mod function.

What's a simple periodic function with a smooth curve?

3 Answers3