Does the matrix exponential have this convexity property?

Question

Let $A$ be a real matrix (not necessarily symmetric) whose off-diagonal elements are all non-negative, so that the elements of the matrix exponential $\exp(A)$ are all non-negative. Let $\mathbf x$ be a vector whose elements are all non-negative. Let $\sum(\cdot)$ denote the sum of all the terms in a vector.

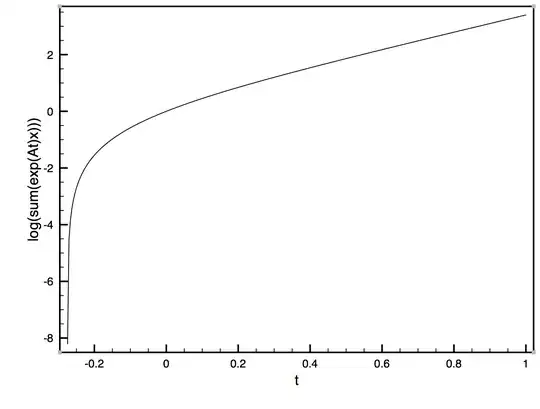
I hypothesise that the function $f(t) = \log \,\sum\big(\exp(At)\, \mathbf x\big)$ is a convex function of $t$.

Note that '$\log$' in this formula is an ordinary logarithm while '$\exp$' is a matrix exponential. From playing around with this I haven't found an easy way to show it, but I haven't found an obvious counterexample either. So my question is, is $f(t) = \log\, \sum\big(\exp(At)\, \mathbf x\big)$ a convex function of $t$, if the entries of $A$ and $\mathbf x$ are non-negative?

For the avoidance of doubt, and for ease of searching for counterexamples, here is some Python code that calculates $f(t)$. (A and x should be numpy arrays of the appropriate dimensions.)

import numpy as np
import scipy.linalg as spl

def f(t, A, x):
    return np.log(np.sum(spl.expm(A*t).dot(x)))

Notes

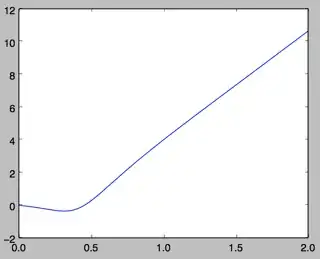
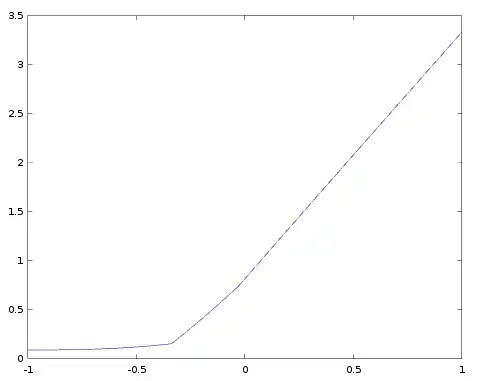
1. Originally I was using the convention that "convex" means a downward curve, i.e. the second derivative is never positive. However, Jonas Meyer points out in a comment that there are examples where the second derivative is consistently positive. So now I guess my question is, can the second derivative of $f(t)$ change sign as a function of $t$?

2. I'm mostly only interested in part of the function where $t>0$, though in examples it seems to work for $t<0$ as well, until the sum of the elements becomes negative.

3. It might be necessary to make additional assumptions about $A$ and $\mathbf x$, e.g. that $\exp(A)$ is irreducible, or that $\mathbf x$ has all positive elements. If that's the case I'd like to know.

4. The motivation has to do with growing populations in biology. It's equivalent to asking whether the per capita rate of population growth is always non-increasing in a simple model of a growing (or shrinking) population.

5. This question is obviously closely related but not the same, and my hypothesis doesn't seem to immediately follow from that result.

6. The result will be true if the elements of $\exp(At)$ are log-convex, which would be a generally useful result to know about if it's true. It turns out not to be the case that all the elements of $\exp(At)$ are either consistently all convex upward or convex downward; they can change from one to the other as a function of $t$. See my related MathOverflow question. This makes me skeptical that the hypothesis in this (Math.SE) question is true.

Here is an example of what it tends to look like. For this example, $$ A = \begin{pmatrix}1,1\\4,1\end{pmatrix}, \qquad \mathbf{x} = \begin{pmatrix}1\\0\end{pmatrix}. $$

Answer 1

Ok, so I can finally put this question to bed with a numerical example. Here is a plot of $\log Z$ against $t$ for some particular non-negative matrix $A$:

The second derivative clearly changes sign twice, once at around 0.3 and again just after 0.5.

It's probably not worth printing the whole matrix here since it's $100\times 100$ and there must be smaller, more instructive examples, but it was generated with the following rather arbitrary Python code:

n = 100
A = np.random.random((n,n)) # should be a Metzler matrix
A = np.exp(W*2)
A = W - np.eye(n)
A[np.random.random((n,n))>0.02] = 1e-3

(The point was to put the leading eigenvalue close to the cloud of other eigenvalues that random matrices tend to exhibit.)

Answer 2

Here is a random counter example:

A =

0.3384042   0.1355143   0.2244029   0.0094600   0.3658720
0.7335746   0.5823969   0.9182229   0.8483730   0.9743839
0.3992142   0.6501968   0.8946143   0.8120155   0.5938882
0.8255626   0.0570781   0.2135843   0.8498636   0.1053567
0.4915833   0.7814256   0.1870035   0.4286809   0.6484581

x =

0.384444
0.441505
0.623156
0.016760
0.791119

This produces this function like this:

Looks pretty convex (although I am not sure if you are probably after concavity), but its not. Around zero there is slightly decreasing derivative…