4

Since I have an interest in polyhedra I've come across https://en.wikipedia.org/wiki/Trigonal_trapezohedron, especially the asymmetric one. So this made me wonder for a classification of convex hexahedron with congruent quadrilateral faces.

Let $P$ be a convex hexahedron with only quadrilateral faces, which are all congruent to each other. I have been able to prove the following:

  • The polyhedral graph of $P$ is the same as the polyhedral graph of a cube.
  • A face of $P$ (thus each face) must have two sides of equal length.
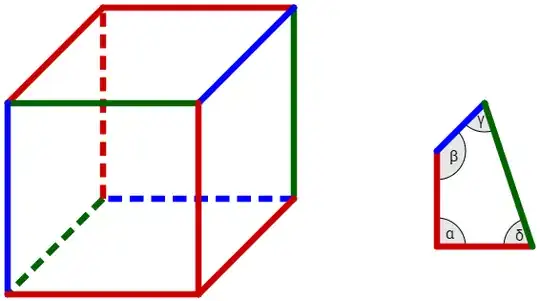
  • The edge configuration of $P$ is depicted in the figure below.

enter image description here

Edges with same colour are of equal length.

The angles $\alpha, \beta, \gamma$ and $\delta=2\pi-\alpha-\beta-\gamma$ completely define such a hexahedron (up to scale). Since the hexahedron is convex, we can get that $\alpha < \frac{2\pi}{3}$.

So my question is: what extra constraints can I get on the angles?

I've tried to use Descartes' theorem on total angular defect, but this gives an empty condition.

Intelligenti pauca
  • 55,765
Simon Marynissen
  • 1,397

1 Answers1

2

Red edges form two equal tetrahedra $VABC$ and $V'A'B'C'$ (see diagram on the left below), whose bases $ABC$ and $A'B'C'$ are parallel equilateral triangles. Let $O$, $O'$ be the centers of the bases and set $VO=V'O'=h$, $OO'=d$ and $OA=1$. Moreover, let $\phi$ be the angle between the projections of $VA$ and $V'A'$ on a base (see diagram on the right, which is seen "from above").

Points $VABA'$ are coplanar if $[(A-V)\times(B-V)]\cdot(A'-V)=0$, which leads to $$ d=h(\cos\phi+\sqrt3\sin\phi-1). $$ Thus, $h$ and $\phi$ completely determine the hexahedron shape. One can readily compute, in particular, your angles $\alpha$, $\beta$ and $\delta$ as a function of $h$ and $\phi$: $$ \cos(\angle AVB)=1-{3\over2(1+h^2)}, \quad \cos(\angle VAA')={1-\cos\phi-hd\over\sqrt{1+h^2}\sqrt{2+d^2-2\cos\phi}}, \quad \cos(\angle VBA')={1+(1/2)\cos\phi-(\sqrt3/2)\sin\phi-hd \over\sqrt{1+h^2}\sqrt{2+d^2+\cos\phi-\sqrt3\sin\phi}}. $$

enter image description here

Intelligenti pauca
  • 55,765
  • Nice idea to use coplanarity. I guess I can find restrictions to $h$ and $\phi$ now (using that cosine is in $[-1, 1]$). Could you give some details about the calculations you made, e.g. the calculation of $d$ and the cosines of $\alpha$, $\beta$ and $\gamma$? – Simon Marynissen Feb 15 '17 at 23:49
  • I did that the obvious way: $$\cos(\angle AVB)={(A-V)\cdot(B-V)\over \overline{VA} ,\overline{VB}},$$ and so on. – Intelligenti pauca Feb 15 '17 at 23:52
  • And then set up a coordinate system such as $O=(0,0,0)$, $V=(0,0,h)$, $O'=(0,0,-d)$, $A=(1,0,0)$, $A'=(\cos\phi,\sin\phi,-d)$, and so on. – Intelligenti pauca Feb 15 '17 at 23:56
  • That makes sense! Thanks for your answers! – Simon Marynissen Feb 15 '17 at 23:58