Irregular analogue of cube and octahedron.

Question

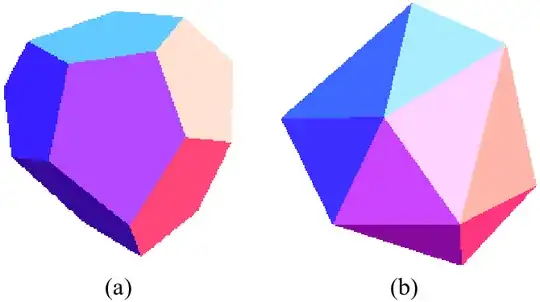
If we take a Dodecahedron and remove the constraint that the pentagonal faces have to be regular pentagons, we get a solid called a Tetartoid. If we take the dual of that, we will end up with the corresponding irregular Icosahedron.

Similarly, there seems to be an irregular analogue for the tetrahedron. However, I've never seen one for the cube and octahedron (which happen to be dual of each other). Is it even possible to have irregular analogues of those two? The criterion is that the solid should be convex with all faces identical and the same number of faces meeting at each vertex. The cube analogue would have six faces which were all quadrilaterals while the octahedron analogue would have eight faces which were all scalene triangles.

EDIT: Actually the Icosahedral object might not necessarily be composed of identical triangles.

See this for an irregular cube: https://math.stackexchange.com/questions/2144830/hexahedron-congruent-faces/ — Intelligenti pauca, Aug 09 '18 at 20:49

Paul Frost · Accepted Answer · 2018-07-29T13:15:09.423

5

For the octahedron it is easy. Take a rhombus $R$ in the $x$-$y$-plane. The diagonals divide it into four congruent scalene triangles. The diagonals intersect in $p$, so shift $p$ in positive $z$-direction and obtain the apex of a pyramid $P$ with base $R$. Reflect $P$ at the $x$-$y$-plane and obtain a pyramid $P'$. Then $T = P \cup P'$ is the desired object. It is obviously obtained by a distortion of the standard octahedron.

For the cube we can proceed similarly and obtain an object with rhombical faces. I do not know whether it is possible to find something with more irregular faces.

edited Jul 29 '18 at 13:15

answered Jul 29 '18 at 10:33

Paul Frost

87,968

Thanks. It was very surprising to me that the dual solid of the irregular Octahedron doesn't satisfy my requirements. I don't understand how you would go about the cube analogue. What 2-D shape would you start with? – Rohit Pandey Jul 29 '18 at 17:52
1

For the cube anlaogue I would start with a rhombus in the $x$-$y$-plane and add congruent rhombi along the edges. It is inelegant to describe this with words. The result is known as the trigonal trapezohedron. See https://en.wikipedia.org/wiki/Rhombohedron. – Paul Frost Jul 29 '18 at 18:40
I construct the same octahedron by a different method. That approach emphasizes that the congruent faces of the octahedron are acute triangles. – Oscar Lanzi Dec 09 '22 at 01:08

score 2 · Answer 2 · answered Jul 29 '18 at 11:49

A cube could be elongated in either of its directions of face normals. this makes some of its faces to rectangles instead.

Alternatively a pair of faces (bases, if considered a square prism) could be sheered wrt each other. This makes some of its faces into parallelograms.

Finally you could squash a cube diametrally (along its body diagonal). This makes all faces into rhombs.

And, for sure, you could combine all theese operations.

--- rk

The OP wants all faces identical. – Ethan Bolker Jul 29 '18 at 13:18 — Ethan Bolker, Jul 29 '18 at 13:18

score 2 · Answer 3 · answered Jul 29 '18 at 18:26

2

See the Wikipedia entry on the rhombohedron for images:

Note the 2nd shape: $6$ identical rhombi.

answered Jul 29 '18 at 18:26

Joseph O'Rourke

31,079

1

Thanks, +1. And in this article - https://en.wikipedia.org/wiki/Trigonal_trapezohedron they also mention quadrilaterals that have two adjacent sides equal can be used to form a cube analogue (not just Rhombi). – Rohit Pandey Jul 29 '18 at 18:44

Oscar Lanzi · Answer 4 · 2024-07-04T13:08:12.637

We prove that an octahedron can be made from eight congruent acute triangular faces.

We begin with the more familiar fact that four congruent triangles can be assembled into the faces of a tetrahedron, if and only if the triangles are acute. Having assembled such a tetrahedron, we now invert it through the (circum)center and superpose this inversion on the original copy. Most readers are familiar with the stellated fugure this produces in the regular case, with a central regular octahedron whose interior is the common interior region of both tetrahedra. The general case discussed here, where the triangles are congruent but may not be equilateral, is an af-fine transformation of the regular form, so again we have a defined central octahedron.

Given that the edges of either tetrahedron are parallel to those of its central inversion, the triangular faces of the central octahedron must be similar to those of the tetrahedra. Thus the congruent acute triangles used to make the original tetrahedron are inherited into the octahedral faces, with the length dimensions reduced by half.

Irregular analogue of cube and octahedron.

4 Answers4