I've recently discovered that modifying the standard Newton-Raphson iteration by "squashing" $\frac{f (t)}{\dot{f} (t)}$ with the hyperbolic tangent function so that the iteration function is
$$N_f (t) = t - \tanh \left( \frac{f (t)}{\dot{f} (t)} \right)$$
results in much larger (Fatou) convergence domains, also known as (immediate) basins of attraction.
The convergence theorems of the Newton-Kantorivich type , such as those in On an improved convergence analysis of Newton’s method can be modified in a relatively straightforward way so that they apply to this modified iteration. For instance, the parameter $\eta$ defining the inequality in the referenced paper,
$$\left\| \frac{F (x_0)}{F' (x_0)} \right\| \leqslant \eta$$
can be replaced with
$$\left\| \tanh \left( \frac{F (x_0)}{F' (x_0)} \right) \right\| \leqslant 1$$
so that $\eta=1$ at most, no matter the (differentiable) function $F(x)$ , since the range of $\tanh(x)$ is $(- 1, 1)$
For the function I am applying this to, the Hardy Z function, $$\begin{array}{ll} Z (t) & = e^{i \vartheta (t)} \zeta \left( \frac{1}{2} + i t \right) \end{array}$$ where $$\vartheta (t) = - \frac{i}{2} \left( \ln \Gamma \left( \frac{1}{4} + \frac{i t}{2} \right) - \ln \Gamma \left( \frac{1}{4} - \frac{i t}{2} \right) \right) - \frac{\ln (\pi) t}{2}$$ this tanh modification has much better convergence properties than the regular Newton iteration when using the starting points, indexed by n, $$x_0 (n) = \frac{2 \pi \left( n - \frac{11}{8} \right)}{W \left( \frac{n - \frac{11}{8}}{e} \right)}$$ where $W(x)$ is the Lambert W function, which is the exact solution to the approximation equation for the Riemann zeros obtained by replacing $\vartheta$ with its Stirling approximation $$\tilde{\vartheta} (t) = \frac{t}{2} \ln \left( \frac{t}{2 \pi e} \right) - \frac{\pi}{8}$$ and solving $$\tilde{\vartheta} (x_0 (n)) = \left( n - \frac{3}{2} \right) \pi$$
However, even with this tanh modification, only about 98.02% of the first 100,000 zeta zeros converged to the n-th zero when started from the n-th approximation zero. The problem for many of these points, is that derivative of the map $$M_f (t_{}) = \frac {d}{d t} N_f (t) = {\frac {1}{ \left( \mbox {D} \left( f \right) \left( t \right) \right) ^{2}} \left( \left( \cosh \left( {\frac {f \left( t \right) }{\mbox {D} \left( f \right) \left( t \right) }} \right) \right) ^{2 } \left( \mbox {D} \left( f \right) \left( t \right) \right) ^{2}+f \left( t \right) \left( D^{ \left( 2 \right) } \right) \left( f \right) \left( t \right) - \left( \mbox {D} \left( f \right) \left( t \right) \right) ^{2} \right) \left( \cosh \left( {\frac {f \left( t \right) }{\mbox {D} \left( f \right) \left( t \right) }} \right) \right) ^{-2}} $$, which is the multiplier of the fixed point when evaluated at a zero of $f(t)$, is quite large when it happens to be near the edge of the basin of attraction, causing the trajectory to jump out of its immediate basin and land in a neighboring one.
I postulated that using the relaxed/damped Newton's iteration with a damping/relaxation factor $h_n$ which was inversely proportional to the multiplier $M_f(x_n)$ would result in much better convergence properties, so I defined the relaxation/damping factor at the m-th step to be $$h_m = \tanh (| M_f (x_m)^{- 1} |)$$ so that the iteration becomes $$N_f (t) = t - \tanh (| M_f (x_m)^{- 1} |)\tanh \left( \frac{f (t)}{\dot{f} (t)} \right)$$
and came to discover that this method of choosing the relaxation parameter results in quite excellent convergence properties.. convergence for about 99.976% of the zeros up to $n=200000$ . I should mention here that I actually use 3 starting points, if an iteration does not convergence from $x_0(n)$ then I try starting from $$\frac{(x_0 (n - 1) + x_0 (n))}{2}$$ and if that doesn't converge, starting from $$\frac{(x_0 (n) + x_0 (n + 1))}{2}$$, and finally if that doesn't converge, declaring the index n to be "not yet convergent" .
My question is, does this unrelaxed tanh iteration have a name or has it been studied? If so, does the method of choosing the relaxation parameter to be inversely proportional to the multipler have a name or has been studied before?
I have no doubt that good starting points exist for every root of $Z$ , and that extending this starting point selection method to do some sort of halving method similar to the bisection method of finding roots would do able to find a good starting point without having to do too much recursive subdividing of the interval $(\frac{(x_0 (n - 1) + x_0 (n))}{2},\frac{(x_0 (n) + x_0 (n + 1))}{2})$
p.s. I'm using the Hardy Z function as an example of a non-polynomial transcendental function with multiple zeros but it should work with any other function that Newton's method works on. If anyone is interested in the code I wrote to do this convergence, then send me a message. It is written in Java using JNA to wrap arblib which is way faster than Maple and does parallel processing to speed up the search. There are 47 indices <200,000 for which the method above converges to the wrong zero, i.e. starting from x0(n) it doesnt converge to x(n) but to some x(m) where m!=n, they are $$[21250, 22700, 28569, 35127, 35388, 48745, 54528, 55646, 62572, 67652, 73777, 80093, 86530, 86914, 88082, 89641, 92548, 96858, 98150, 100494, 103940, 104782, 115986, 120067, 128690, 130098, 132607, 133231, 141441, 141695, 147020, 149253, 152984, 155057, 156849, 158729, 163891, 164016, 165178, 171748, 175284, 180607, 182832, 187463, 190452, 192768, 196874]$$
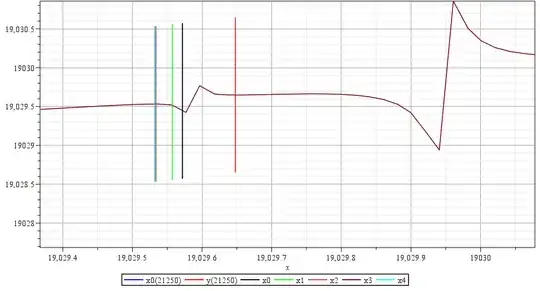
For example, here is a graph of the iteration near the 1st non-convergent point n=21250
x0 := 19029.571920834291724
h1 := .15057973742585188810
x1 := 19029.557342014086776
h2 := 0.63772212783089483930
x2 := 19029.533810633781735
h3 := 1.
x3 := 19029.532171164322700
h4 := 1.
x4 := 19029.532198342701094
p.s. this type of convergence analysis applied to the Grampoints was more straightforward . See Convergence of the Newton-Kantorovich Method for the Gram Points