4

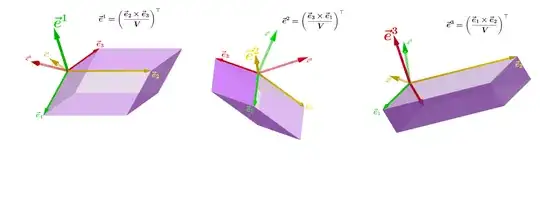
In this Wikipedia entry there is an example and a formula to calculate the dual basis for a basis in $3-$dim Euclidean space. I copy here for convenience:

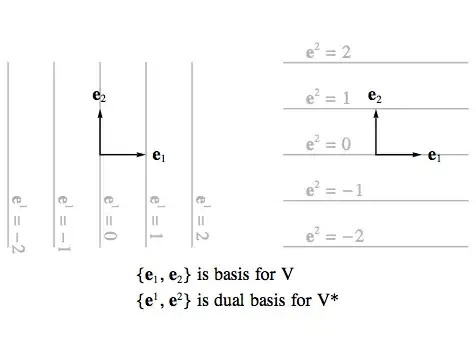
For example, the standard basis vectors of $R^2$ (the Cartesian plane) are

$\displaystyle \{\mathbf {e} _{1},\mathbf {e} _{2}\}=\left\{{\begin{pmatrix}1\\0\end{pmatrix}},{\begin{pmatrix}0\\1\end{pmatrix}}\right\}$

and the standard basis vectors of its dual space $R^{2*}$ are

$\displaystyle \{\mathbf {e} ^{1},\mathbf {e} ^{2}\}=\left\{{\begin{pmatrix}1&0\end{pmatrix}},{\begin{pmatrix}0&1\end{pmatrix}}\right\}{\text{.}}$

In 3-dimensional Euclidean space, for a given basis $\{e_1, e_2, e_3\}$, you can find the biorthogonal (dual) basis $\{e^1, e^2, e^3\}$ by formulas below:

$\displaystyle \mathbf {e}^{1}=\left({\frac {\mathbf {e}_{2}\times \mathbf {e} _{3}}{V}}\right)^{\text{T}},\ \mathbf {e}^{2}=\left({\frac {\mathbf {e} _{3}\times \mathbf {e}_{1}}{V}}\right)^{\text{T}},\ \mathbf {e} ^{3}=\left({\frac {\mathbf {e}_{1}\times \mathbf {e} _{2}}{V}}\right)^{\text{T}}.\tag 1$

where T denotes the transpose and

$\displaystyle V\,=\,\left(\mathbf {e} _{1};\mathbf {e} _{2};\mathbf {e} _{3}\right)\,=\,\mathbf {e} _{1}\cdot (\mathbf {e} _{2}\times \mathbf {e} _{3})\,=\,\mathbf {e} _{2}\cdot (\mathbf {e} _{3}\times \mathbf {e} _{1})\,=\,\mathbf {e} _{3}\cdot (\mathbf {e} _{1}\times \mathbf {e} _{2})$ is the volume of the parallelepiped formed by the basis vectors $\displaystyle \mathbf {e} _{1},\,\mathbf {e} _{2}$ and $\displaystyle \mathbf{e}_{3}.$

To avoid misunderstandings, Eq.$(1)$ says that the cross product of every combination of the basis vectors (for example $\mathbf e_2 \times \mathbf e_3$, which would yield a vector with magnitude equal to the surface of the parallelogram defined by the vectors $\mathbf e_2$ and $\mathbf e_3$), scaled down by the volume of the parallelepiped $V$ will result in a different basis vectors element for the dual space (after transposing).

If all this is true, then the question is,

What is the geometrical interpretation in the case of the standard basis both for 2D and 3D, as well as with any basis vectors in 3D? I imagine this could be a representation of the covectors of a basis in 3D...

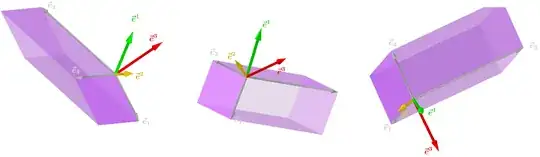
enter image description here

This picture is in reference to a comment, and portrays the basis covectors from two views:

enter image description here

Community
  • 1
Antoni Parellada
  • 10,239
  • 1
    Usually there is no natural isomorphism of a vector space and it's dual, you just know they are isomorphic. Once you introduce a scalar product on a vector space $V$ (which means a construction to calculate lengths and angles) it turn out that the mapping $v\mapsto \langle v, . \rangle$ is a natural isomorphism of $V$ with it's dual. Because it is derived from a scalar product one should expect that this particular isomorphism relates length, area and volume to algebraic constructions on the dual. Some of them you have written down. The standard basis is orthonormal wrt the scalar product. – Thomas Feb 11 '17 at 15:59
  • This Wikipedia entry might be helpful. – amd Feb 11 '17 at 19:43

1 Answers1

6

Given the standard vector basis $\displaystyle \{\mathbf {e} _{1},\mathbf {e} _{2}\}=\left\{{\begin{pmatrix}1\\0\end{pmatrix}},{\begin{pmatrix}0\\1\end{pmatrix}}\right\}$ we can interpret the dual basis $\displaystyle \{\mathbf {e} ^{1},\mathbf {e} ^{2}\}=\left\{{\begin{pmatrix}1&0\end{pmatrix}},{\begin{pmatrix}0&1\end{pmatrix}}\right\}{\text{.}}$ as two families of straight lines orthogonal to the vectors of the basis, as in this figure (from here).

enter image description here

In this interpretation the linear functional $e^1(\vec v)$ is a number that count the number of lines crossed by the vector.

In a similar fashion we ca interpret a dual basis and a linear functional in three dimensions, as you can see in the figure at this page of Wikipedia (note that a one-form is essentially the same as a linear functional).

I think that, looking at these pictures, you can interpret the definition of the dual basis that you have cited.

I use the term ''interpret'' because the elements of the dual space $V^*$ of a vector space $V$ are not the vectors of $V$, but the linear functionals on this space. So your picture is correctonly if we interpret the elements $e^i$ not as vectors, but as direction in which the projections of vectors of $V$ are measured. This is the reason because I prefer to think at the linear functionals as a family of lines (or planes, in a $3D$ space), that are othogonal to the vectors $e^i$ in your figure. Clearly the vector used in your figure identify exactly the plane of the linear form, so they identify a basis if they are linearly independent. In other word, the the operation of transposition, from a vector $ v$ to $v^T$ is interpreted as the change from a vector that define a direction and a unit of mesure in such direction, to a set of planes orthogonal to such direction, whose distance is measured in the same unity (note that also the figure in the comment of @amd use a set of plane for the dual basis).

Last: this interpretation of the dual space is useful becausecanbe extended from the 1-forms ( that are the same as the linear functionals) to n-forms as is suggested here (and you can see better reading the answers here)

Community
  • 1
Emilio Novati
  • 64,377
  • Emilio, I like your exposition very much, but why do we have to "interpret" the basis of the dual? In generalized curvilinear spaces, they are real vectors orthogonal to the tangents to the displacement vectors (I think this is in the comment with a link under the OP). It is confusing because they are also functions (or functionals)... Also, I included an image that took me hours to put together, basically encapsulating that the basis of $V^*$ in 3D are the result of a cross product. Is the image correct? – Antoni Parellada Feb 11 '17 at 23:14
  • Your figure is correct, but the problem is the ''interpretation'' . I've added something to my answer to avoid a too long comment. – Emilio Novati Feb 12 '17 at 18:19
  • Your extended comment is very useful. Just one possible typo (?) - on your addition or edit, the second $e^i$, wouldn't it be $e_i$: "I prefer to think at the linear functionals as a family of lines (or planes, in a 3D space), that are othogonal to the vectors $\mathbf e_i$ in your figure."? – Antoni Parellada Feb 12 '17 at 18:30
  • I have posted 3 questions on this topic over the weekend. Your answer and follow-up have been great, so I would like to bring to your attention a bounty of hard-earned 100 points I just posted on my original question on this topic. – Antoni Parellada Feb 12 '17 at 20:22
  • I suppose that in your figure the vector $e^1$ is orthogonal to $e^2$ and $e^3$ and normalized such that $\langle e^1,e_1\rangle=1$, or, in the notation of linear functionals, $e^1(e_1)=1$ (this is because the cross product is divided by the volume $V$). In this case the linear functional is defined by the planes orthogonal to this vector $e^1$. Note that if ${e_1,e_2,e_3}$ is an orthonormal basis, than your $e^i$ are the same as $e_i$ (thinked as vectors). They becames different only for a non orthonormal basis. – Emilio Novati Feb 12 '17 at 20:54
  • Actually no, each one of the $\vec e^{\text {upstairs}}$ is orthogonal to the the plane formed by the other two $\vec e_{\text{downstairs}}$, so $e^{\Large 1}$ is orthogonal to the plane formed by $e_{\Large 2}$ and $e_{\Large 3}$, but I don't think $e^1$ is orthogonal to $e^2$ and $e^3$ (I just added an additional image with only the $e^{\text{upstairs}}$ vectors in the OP). – Antoni Parellada Feb 12 '17 at 21:24
  • Yes, My typo!.. I wrote the index at the top but i was thinking down. :) – Emilio Novati Feb 12 '17 at 21:41
  • Emilio, I was sure of it... I know you understand this, and I don't. Since the topic is a mess of indices, can you re-write your comment? – Antoni Parellada Feb 12 '17 at 21:43
  • I say that your $e^1$ is a vector orthogonal to $e_2$ and $e_3$ and with norm $||e^1||=1/||e_1||$. You agree? – Emilio Novati Feb 12 '17 at 22:00