1

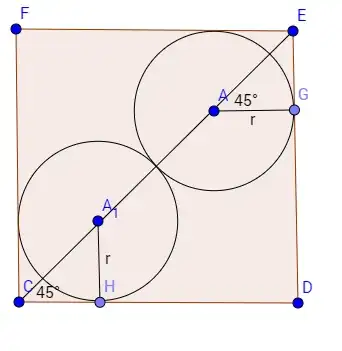
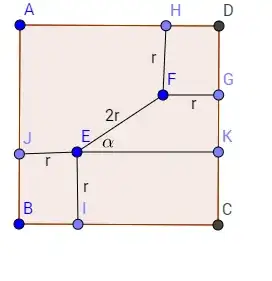
A man has a square piece of paper where each side has length $1$ m. Two equal circles are to be cut from this paper. What is the radius, in meters, of the largest possible circles?

This is what I did:

  • area of square: $1$

  • area area of circle: $2\pi(r^2)$

I multiplied by $2$ since they are $2$ circles. Now I made $2\pi r^2=1$ and solved for $"r"$, however the answer I got is completely off. May you please tell me what I did is wrong and how I can fix that?

Subhash Chand Bhoria
  • 1,006
  • 5
  • 14
user408113
  • 223
  • See http://www2.stetson.edu/~efriedma/cirinsqu/ – Watson Jan 27 '17 at 17:57
  • 1
    How on earth are you going to cut those two circles such that they have the same area as the square? There's got to be wasted paper. – Kaynex Jan 27 '17 at 18:04
  • @watson there is absolutely no logic in providing this link... i posted the question since i want an explanantion – user408113 Jan 27 '17 at 18:04
  • Why did you think that the area of two circles should be equal to the area of the square? This may be helpful:https://en.wikipedia.org/wiki/Circle_packing_in_a_square – Seyed Jan 27 '17 at 18:10
  • The logic behind Watson's posting of that link is blindingly obvious. Your circles have to fit inside the square without overlapping, as the 2nd picture on that page shows. What you did that was wrong was assume that the shape of the circles didn't matter and somehow it was possible to include all of the area of the square inside them. – Paul Sinclair Jan 27 '17 at 18:16
  • @PaulSinclair thank u vvvvv much for ur thoughtful explanation – user408113 Jan 27 '17 at 18:20
  • Obviously the longest distance between the center of two circles is on the diagonal of the square, therefore the largest circles are on the diagonal of the square. – Seyed Jan 27 '17 at 18:21
  • @seyed hello seyed. the diagonal of the square is sqrt2, now how can that help meeee??????????? – user408113 Jan 27 '17 at 18:28
  • It's interesting: the problem doesn't say that the circles have to be cut out in single pieces. For instance, you could cut four half-circles, each with its center on the midpoint of an edge, to assemble two equal circles, and perhaps do somewhat better than the "obvious" answer (I haven't actually checked!). We all know what the question's author intended, but what was said was actually a bit ambiguous. In the limit of clever cutting/and-gluing (for this interpretation), OP's answer is correct. – John Hughes Jan 27 '17 at 18:28
  • @JohnHughes yes i agree, however this question is from a uni so i doubt theyre asking us to cut them into pieces as it would be a v easy q – user408113 Jan 27 '17 at 18:31
  • @exchangehelpforuni : my link provides shows some interesting generalizations, so it was perfectly fine. Moreover, saying "there is absolutely no logic in providing this link" is quite rude, in my opinion. – Watson Jan 27 '17 at 19:03
  • @Watson - ok, here's a better reason why links aren't helpful: the link is now dead. Thankfully, there's the Internet Archive. Here's the archived page. – ashleedawg Dec 14 '21 at 10:37
  • @ashleedawg : yes, thanks (but links are helpful in general, it is only a problem when they are dead, in which case archive.org may save us). In fact the current webpage is https://erich-friedman.github.io/packing/index.html. – Watson Dec 14 '21 at 13:23

1 Answers1

5

enter image description here

That is the picture that fits the problem.

See that

$$CE=\sqrt{2}=CA_1+A_1A+AE=\sqrt{2}r+2r+\sqrt{2}r \to r=\frac{\sqrt{2}}{2+2\sqrt{2}}=\frac{2-\sqrt{2}}{2}$$

EDIT

Hint

To prove that it is the maximum work with the picture below:

enter image description here

Work with variation of $\alpha$, the trapezium $EFGK$ and $DG+GK+KC=DC=1$.

Arnaldo
  • 21,758
  • 1
    What tool did you use to draw the figure, please? – John Hughes Jan 27 '17 at 18:40
  • @JohnHughes: Geogebra (https://www.geogebra.org/apps/) – Arnaldo Jan 27 '17 at 18:41
  • @JohnHughes: you are very welcome! – Arnaldo Jan 27 '17 at 18:44
  • Intuitively this is what I thought the answer would be, but it's not exactly a proof. Can you prove that this is the optimal choice of circles? – Vik78 Jan 27 '17 at 19:18
  • @Vik78: you are right! I made a update as a hint. – Arnaldo Jan 27 '17 at 19:37
  • @Vik78: I think it is not that difficult to finish. – Arnaldo Jan 27 '17 at 19:41
  • It's a very nice picture, but this is still not a complete answer. I lack the geometric experience to see what you're hinting at. – Vik78 Jan 27 '17 at 19:56
  • 1
    @arnaldo thank YOU VERY much!!!! very very helpful!!! Btw u did not need that second picture titled "hint" i think some users r just challenging you. – user408113 Jan 27 '17 at 20:31
  • @exchangehelpforuni: you are very welcome! – Arnaldo Jan 27 '17 at 20:32
  • @arnaldo i think ur good with geomtery, may u plz help me with my other question? – user408113 Jan 27 '17 at 20:36
  • @exchangehelpforuni: Sure! Post your question and I will try to help you! But don't forget to write what you tried so far! – Arnaldo Jan 27 '17 at 20:38
  • Thank you!!! Here is the question, i already posted it http://math.stackexchange.com/questions/2116854/largest-equilateral-triangle-which-fits-inside-a-square?noredirect=1#comment4353433_2116854 – user408113 Jan 27 '17 at 20:39
  • @exchangehelpforuni: Unfortunately I can't help you with that because it is marked as duplicated. You can check the solution here: http://math.stackexchange.com/questions/59616/find-the-maximum-area-possible-of-equilateral-triangle-that-inside-the-given-squ – Arnaldo Jan 27 '17 at 20:41
  • @arnaldo i checked that answer but it does not contain anything valuabel – user408113 Jan 27 '17 at 20:41
  • @Arnaldo pleaseeeee pleaseee is there any way you can help me with this question??? Can we comment on the other post??? Even though its 5 years old – user408113 Jan 27 '17 at 20:42