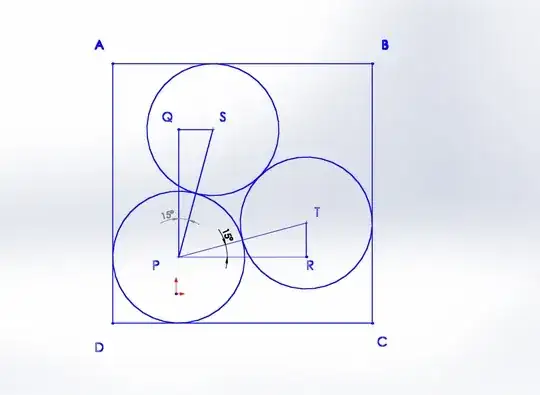
N circles of maximum possible equal radius are contained in a square of side 1 with no overlap among the circles. What is the % of the area of the square outside the circle for N=3? (would appreciate a way of thinking about solving this for the general case; also, is there an easy way to extrapolate this into higher dimensions? i.e. spheres of maximum possible equal radius inside a cube of side 1).
This is similar to the question here, but I am looking for a generalized way of thinking about this, for circles and cubes: Maximum area of $2$ circles in a square Thank you.