There is a circle of radius R, and 2 chords intersect perpendicularly inside the circle. The distance from the center of the circle to each chord is known (h and w).
Looking for derivations of 3 individual expressions A(R,h,w) for areas of the 3 numbered regions in the circle shown below.
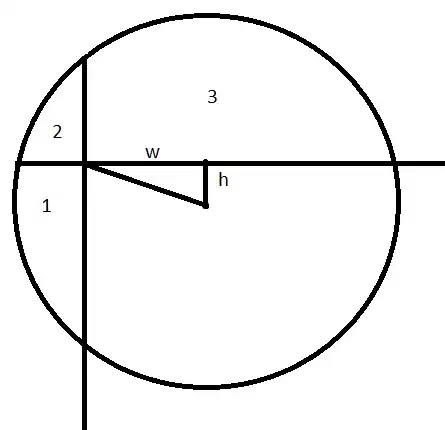
The individual expressions are quite complicated to type out expicitly in mathjax, but can be deduced from the following, using the standard result for the area of a segment:
Firstly, $$A_1+A_2=\frac 12R^2(2\theta-\sin2\theta)$$ where $\cos\theta=\frac wR$ so $\sin2\theta=2\frac{w\sqrt{R^2-w^2}}{R^2}$
Likewise, $$A_2+A_3=\frac 12R^2(2\phi-\sin2\phi)$$ where $\cos\phi=\frac hR$ so $\sin2\phi=2\frac{h\sqrt{R^2-h^2}}{R^2}$
And furthermore, $$A_1+A_2+A_3=\pi R^2-\Delta-A_4$$ where $$\Delta=\frac 12(w+\sqrt{R^2-h^2})(h+\sqrt{R^2-w^2})$$ and $$A_4=\frac 12R^2(\psi-\sin\psi)$$ where $\psi=\frac{3\pi}{2}-\theta-\phi$
Enjoy...
