9

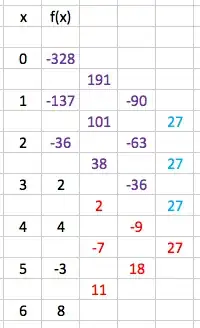
Question: Is there an easier way to solve this problem?

Suppose the polynomial $f(x)$ is of degree $3$ and satisfies $f(3)=2$, $f(4)=4$, $f(5)=-3$, and $f(6)=8$. Determine the value of $f(0)$.

My Attempt: I started off with the general cubic $ax^3+bx^2+cx+d=f(x)$ and manually plugged in each point to get the following system:$$\begin{align*} & 27a+9b+3c+d=2\\ & 64a+16b+4c+d=4\\ & 125a+25b+5c+d=-3\\ & 216a+36b+6c+d=8\end{align*}\tag1$$

Solving the system with the handy matrix gives the solutions as $a=\frac 92,b=-\frac {117}2,c=245,d=-328$. Thus, $f(0)=-328$.

Even though I (think) solved the problem correctly, this method seems a bit "bulky" especially when everything becomes a higher degree. So I'm wondering if there is a quicker way to evaluate this kind of problem.

Community
  • 1
Frank
  • 6,594

3 Answers3

16

Linear functions (degree $1$ polynomials) $p(x)$ have constant first differences $(\Delta^1f)(x)=f(x)-f(x-1)$, quadratic functions have constant second differences $(\Delta^2f)(x)=(\Delta^1f)(x)-(\Delta^1f)(x-1)$, and so on. You can use this fact to find $f(0)$ as shown below. First, from the known values, calculate the forward differences (red) from left to right, then copy the constant third difference (blue), and finally “back-calculate” to $f(0)$ (purple).

enter image description here

Steve Kass
  • 15,314
7

There is a conceptually simpler way: do some linear algebra and polynomial arithmetic. Instead of a complex linear system, solve $4$ much simpler linear systems. Namely, solve the following problems: find polynomials $p(x), q(x), r(x), s(x)$ such that: \begin{align} (a)\enspace&\begin{cases}p(3)=1\\p(4)=0\\p(5)=0\\p(6)=0\end{cases} &(b)\enspace&\begin{cases}q(3)=0\\q(4)=1\\q(5)=0\\q(6)=0\end{cases} &(c)\enspace&\begin{cases}r(3)=0\\r(4)=0\\r(5)=1\\r(6)=0\end{cases} &(d)\enspace&\begin{cases}s(3)=0\\s(4)=0\\s(5)=0\\s(6)=1\end{cases} \end{align} Then the solution is $$f(x)=2p(x)+4q(x)-3r(x)+8s(x).$$

Reminder:

Let $K$ be a field, $\alpha\in K$, $f(x)$ a polynomial in $K[x]$. Then, $$f(\alpha)=0\iff x-\alpha\enspace\text{divides}\enspace f(x).$$

Bernard
  • 179,256
  • That's nice!${}{}$ – TonyK Nov 27 '16 at 02:06
  • 2
    From the linear algebra point of view, those systems aren't really simpler; they all have the same matrix. There is a fast way to solve them using the zeros of polynomials, but you should mention it in your answer, otherwise I am afraid it is not very helpful as it stands. – Federico Poloni Nov 27 '16 at 09:04
  • @Federico Poloni: You're right.. I supposed everyone has this result in mind, but it's not very realistic. Thanks for drawing my attention to this point! – Bernard Nov 27 '16 at 12:38
5

You can directly find out the polynomial $f$ by considering it according as the $x$-values available:

Let $f(x)=a_0+a_1(x-3)+a_2(x-3)(x-4)+a_3(x-3)(x-4)(x-5)$ for real constants $a_0,a_1,a_2,a_3$. Note that we don't need to take into account the value $x=6$ as this is already a cubic polynomial.

Then, $f(3)=2\Rightarrow a_0=2$

$f(4)=4\Rightarrow a_1=2$

$f(5)=-3\Rightarrow a_2=-\frac{9}{2}$

$f(6)=8\Rightarrow a_3=\frac{9}{2}$

Thus, $f(x)=2+2(x-3)-\frac{9}{2}(x-3)(x-4)+\frac{9}{2}(x-3)(x-4)(x-5)$.

I think the calculations are pretty simple this way as you have chosen $f$ to be such.

StubbornAtom
  • 17,932