Cauchy integral with singularity on contour

Question

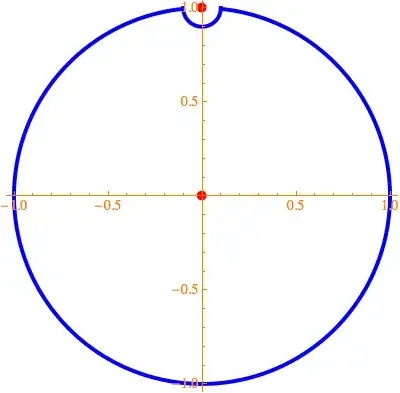
I have been trying to calculate

$$ I = \oint_C {\rm d}z\; \frac{e^z}{z^2(z-i)} = \oint_C {\rm d}z\; f(z) $$

with $C = \{z : |z|^2 = 1\}$ (the unit circle). The function $f$ has a simple pole on $C$, so I changed the contour a bit to avoid this singularity, the figure below shows a sketch

I did this inspired by this other question. Now I split my new integration contour into two:

• $C_1 = \{z: z = e^{i\theta},\; \pi/2 + \epsilon <\theta<5\pi/2 + \epsilon \}$

This is the result I get

$$ I_1 = \lim_{\epsilon \to 0} \int_{C_1}{\rm d}z\;f(z) = i\pi e^i \tag{1} $$

• $C_2 = \{z: z = i + \epsilon e^{i\theta},\; -\pi <\theta<0 \}$

$$ I_2 = \lim_{\epsilon \to 0} \int_{C_2}{\rm d}z\;f(z) = 2\pi(i - 1) -2\pi i e^i \tag{2} $$

Now, because I avoided the singularity at $z=i$, the only pole that contributes to the residues should be $z=0$

$$ {\rm Res}(f,0) = 1 + i \tag{3} $$

The problem that I have is that

$$ I = I_1 + I_2 = 2\pi(i-1) -\pi i e^i $$

while, by using Cauchy's theorem, I expect

$$ I = 2\pi i (i + 1) $$

Any hints?

Answer 1

You should get different results as you approach the singularity from outside and inside the contour. A relevant result is that the Sokhotsky-Plemelj formulas state that the difference in the value of a Cauchy integral as you approach from the left and from the right is always equal to $2\pi f(z_0)$. Since you probably want the principal value of the integral, you should average the values you get from approaching from outside the contour and approaching from inside the contour.