3D geometric interpretations of matrix inverse

Question

In the question Geometric interpretations of matrix inverses, I provided a visual answer for the $2 \times 2$ case, showing the relationship between the matrices $A$ and $A^{-1}$ in terms of the size and shapes of the parallelograms of their row vectors.

I've completed a parallel demonstration for the inverse of a $3 \times 3$ matrix, shown below, but I would like to characterize the relationship more completely than I did before. For example,

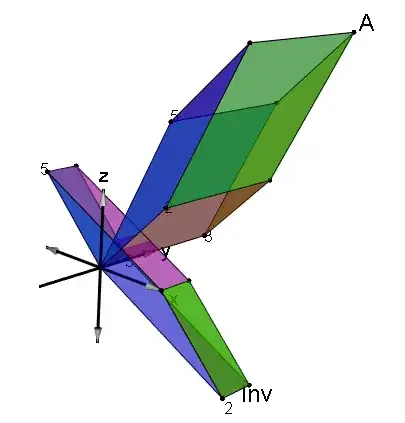
• What is a general statement of the orthogonality relations between the (row) vectors $a_1$, $a_2$, and $a_3$ that define the paralellepiped of $A$ to the corresponding vectors $a^1$, $a^2$, and $a^3$ of $A^{-1}$?

• Are there interesting relations between dot (inner) products and cross-products of the vectors $a_i$ and $a^i$?

• How can one describe the relationships between the faces of $A$ and $A^{-1}$?

In this example, I use the following matrix A, whose determinant is 2.

     [,1] [,2] [,3]
[1,]    1    0    1
[2,]    0    2    0
[3,]    1    0    2 

Its inverse is:

     [,1] [,2] [,3]
[1,]    2  0.0   -1
[2,]    0  0.5    0
[3,]   -1  0.0    1

Here is a 3D plot of $A$ and $A^{-1}$, with axes and some corresponding vertex points labeled. Faces are colored in the same way on both views.

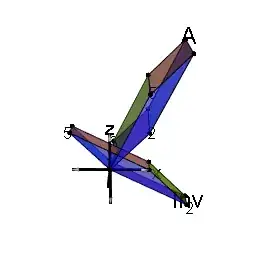
Here is an animated version of the same, rotating around the $z$ axis.

In case anyone is interested, these figures are done in R, and the code for this example is in this gist