22

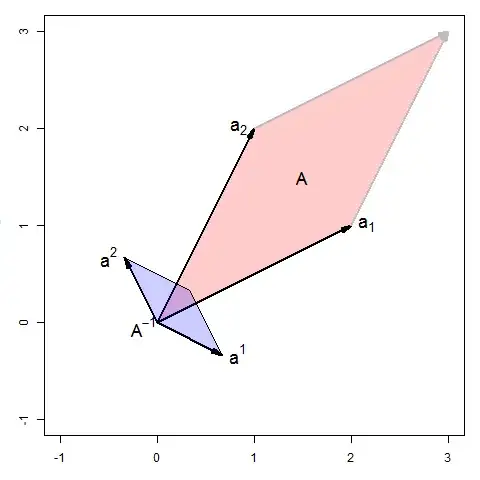
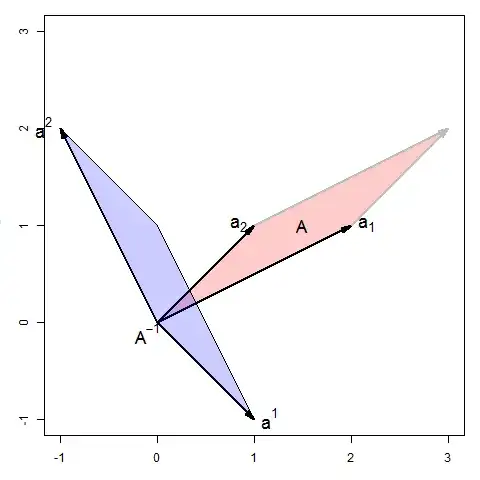
Let $A$ be an invertible $n \times n$ matrix. Suppose we interpret each row of $A$ as a point in $\mathbb{R}^n$; then these $n$ points define a unique hyperplane in $\mathbb{R}^n$ that passes through each point (this hyperplane does not intersect the origin).

Under this geometric interpretation, $A^{-1}$ has an interesting property: the normal vector to the hyperplane is given by the row sums of $A^{-1}$ (i.e. $A^{-1} \cdot 1$, where $1 = \langle 1, \dots, 1 \rangle^T$).

Within this geometric interpretation of $A$, what other interesting properties does $A^{-1}$ have? Do the individual entries of $A^{-1}$ have geometric meaning? How about the column sums?

Rodrigo de Azevedo
  • 23,223
GMB
  • 4,256
  • 1
    Well, the column sum of $A^{-1}$ is the row sum of $(A^{-1})^T$, so since $A^T (A^{-1})^T = I$, there is a similar geometric interpretation. – Daniel Pietrobon Feb 05 '13 at 08:21
  • 2
    Maybe this could be of some use: http://ofekshilon.com/2013/01/11/geometric-interpretation-of-a-3d-matrix-inverse/ – PhD Oct 14 '13 at 18:57
  • answer is here http://mathoverflow.net/questions/120884/geometric-interpretations-of-matrix-inverses – Creator Apr 22 '16 at 22:05

2 Answers2

17

Here is a visual answer for the $2\times 2$ case.

  • Plot the row (or column) vectors, $a_1, a_2$ of $A$ in $\mathcal{R}^2$ to visualize $A$. The area of the parallelogram they form is of course $\det(A)$.
  • In the same space, plot the row (or column) vectors $a^1, a^2$ of $A^{-1}$, and the area of their parallelogram is then $\det(A^{-1}) = 1/ \det(A) $.
  • The relationship between the two illustrates various properties of the matrix inverse.

An example is shown in the picture below, which comes from the matrix (in R notation)

A <- matrix(c(2, 1, 
              1, 2), nrow=2, byrow=TRUE)

In the R package matlib I recently added a vignette illustrating this with the following diagram for this matrix.

inverse diagram

Thus, we can see:

  • The shape of $A^{-1}$ is a $90^o$ rotation of the shape of $A$.

  • $A^{-1}$ is small in the directions where $A$ is large

  • The vector $a^2$ is at right angles to $a_1$ and $a^1$ is at right angles to $a_2$

  • If we multiplied $A$ by a constant $k$ to make its determinant larger (by a factor of $k^2$), the inverse would have to be divided by the same factor to preserve $A A^{-1} = I$.

I wondered whether these properties depend on symmetry of $A$, so here is another example, for the matrix A <- matrix(c(2, 1, 1, 1), nrow=2), where $\det(A)=1$.

enter image description here

It would be interesting to extend this to other properties and to the $3 \times 3$ case, which I leave to others.

user101089
  • 509
  • 3
    Not all your observations are true in the general case. The 90° thing for example. You just got lucky with your numbers. For example $A = [[-1, 0], [-3, 2]]$, $A^{-1} = [[-1, -0. ], [-1.5, 0.5]]$ $A_1 \cdot A^{-1}_2 = -1.5 \neq 0 $. Note: internal brackets are rows. – user3578468 May 25 '19 at 02:42
14

It turns out that an answer for the $3 \times 3$ case has similar properties and is also illuminating.

  • Start with a unit cube, representing the identity matrix. Show its transformation by a matrix $A$ as the corresponding transformation of the cube.

  • This also illustrates the determinant, det(A), as the volume of the transformed cube, and the relationship between $A$ and $A^{-1}$.

In R, using the matlib and rgl package, the unit cube is specified as

library(rgl)
library(matlib)
# cube, with each face colored differently
colors <- rep(2:7, each=4)
c3d <- cube3d()
# make it a unit cube at the origin
c3d <- scale3d(translate3d(c3d, 1, 1, 1),
               .5, .5, .5)

A $3 \times 3$ matrix $A$ with $\det(A)=2$ is

A <- matrix(c( 1, 0, 1, 
               0, 2, 0,  
               1, 0, 2), nrow=3, ncol=3)

Extending the 2D idea from the answer above of drawing the images of $A$ and $A^{-1}$ together to 3D, we get the following, best viewed as an animated graphic. The faces of the parallelpiped representing $A^{1}$ are colored identically to those of $A$, so you can see the mapping from one to the other.

inv-demo.gif

user101089
  • 509