1

I've been experimenting around with companion matrices a little bit lately, this time tried to solve matrix polynomial equations. (Something I have no theoretical foundation for why it should work).

Anyway if we consider one of the simplest equations $${\bf T}^2-{\bf C = 0}$$ for ${\bf T , C}\in {\mathbb R}^{2\times 2}$, (where $\bf T$ is what we want to solve for).

It should have the companion matrix

$${\bf M}=\left[\begin{array}{cccc} 0&0&C_{11}&C_{12}\\ 0&0&C_{21}&C_{22}\\ 1&0&0&0\\ 0&1&0&0 \end{array}\right]$$

since ${\bf I}_2$ in the lower left corner corresponds to 1 for $2 \times 2$ matrices. But this does not give me any reasonable solutions when I calculate a random $4\times 2$ matrix $\bf v$ and calculate

$$-({\bf M}^{10}{\bf v})_{3:4,:}\backslash ({\bf M}^{10}{\bf v})_{1:2,:}$$

Any Ideas why it does not work?

mathreadler
  • 26,534
  • In order to solve polynomial matrix equation you should reduce this equation to the generalized eigenvalue problem. The companion matrix will not help you much. – Pawel Kowal Aug 28 '16 at 02:14
  • Actually companion matrices seem to work at least if we allow ourselves to use vectorization of matrices and Kronecker product expansions of matrix multiplication as shown in my answer. – mathreadler Aug 28 '16 at 11:25
  • 1
    Wilkinson's book gives a method to linearize a matrix polynomial into a (Frobenius) companion matrix. Recently, there has also been research to generalize the Fiedler companion matrix to matrix polynomials as well. Linearizations do seem to be an active area of research. – J. M. ain't a mathematician Oct 23 '17 at 17:58
  • @J.M.isnotamathematician that sounds very interesting and indeed I have thought something like that should be possible. Please give some references or pointers where I can read more if you have any. – mathreadler Oct 24 '17 at 08:14

1 Answers1

0

There may exist ways to make the above approach work, but I have not managed to find one yet.

Instead the idea that left and right multiplication does different things lead me to believe we would need another approach. Instead we adopt the vectorization and Kronecker product approach used in some previous questions and answers.

$$\left[\begin{array}{cc} {I_2\otimes {\bf 0}}&-(I_2\otimes {\bf C}^T)\\I_2\otimes I_2&I_2\otimes \bf 0 \end{array}\right]$$

Since our small 2 degree polynomial for $2\times 2$ matrix is so small we can show it explicitly:

$${\bf M}=\left[\begin{array}{rrrr|rrrr}\epsilon&0&0&0&-C_{11}&0&-C_{21}&0\\0&\epsilon&0&0&0&-C_{11}&0&-C_{21}\\0&0&\epsilon&0&-C_{12}&0&-C_{22}&0\\ 0&0&0&\epsilon&0&-C_{12}&0&-C_{22}\\\hline 1&0&0&0&\epsilon&0&0&0\\0&1&0&0&0&\epsilon&0&0\\0&0&1&0&0&0&\epsilon&0\\0&0&0&1&0&0&0&\epsilon\end{array}\right]$$

Please note the $+\epsilon{\bf I}$ we added to slightly push the eigensystem as explained by Robert Israel.

This also lets us decide if each multiplications by $\bf C$ is from the left or from the right. It should make no practical difference in this case since $\bf C$ is not multiplied onto $\bf T$ from any direction, but for other equations it will make a difference. The difference from before is that our right vector will be $(2\cdot 4)\times 1$ this time. We also need to do a devectorization to make sense of the result.

It is also easy to extend, for example solving ${\bf T}^2-\bf C_2T-C =0$ (where would we put the elements to $\bf C_2$ in the matrix above?) For example solving :

$${\bf T}^2-\left[\begin{array}{cc} 0.4152969&-0.302774\\ 1.296701&0.4620149 \end{array}\right]{\bf T}-\left[\begin{array}{cc} -1.594623&0.4579296\\ 2.536964&-2.300262 \end{array}\right]={\bf 0}$$

gives us the solution ${\bf T} = \left[\begin{array}{cc}-1.55046838107395&1.02247507618352\\-3.50309793756543&1.86219643308248\end{array}\right]$

With absolute element errors < $10^{-14}$, quite close to the double precision arithmetics used.

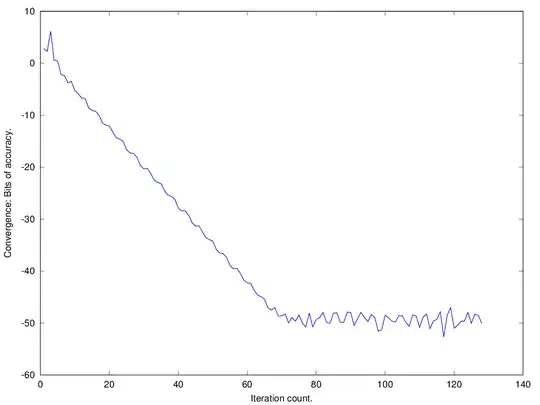enter image description here Convergence plot in a case when $\bf C, C_2$ admit for a real solution. Notice the convergence is both exponential and stops at error of $2^{-50}$: close to the mantissa of 52 bits for double precision floats.

Community
  • 1
mathreadler
  • 26,534