About a mysterious sequence who seems to follow some patterns

Question

This question is maybe linked to this other question.

---

We can prove using the density of some additives sub-groups of $\mathbb R$ that we can approach an integer with a rational of the form $\displaystyle \frac{2^a}{3^b}$.

For a given integer $n$, let's get interesting of the approximation of this form with $b \ge 0$ and $a$ minimal:

$$\left\lfloor \frac{2^a}{3^b}\right\rfloor=n \qquad b \ge 0 \text{ and } a \text{ is minimal},$$

where $\lfloor.\rfloor$ denotes the floor function.

The term minimal here is meaning that we are interesting in a couple $(a,b)$ like that, such that every other $(a',b')$ couple like that won't match the condition if $a'<a$.

Definition 1

We denote $(p_n)_{n\geq 1}$ the sequence defined by

$$\forall n\geq 1, \quad p(n):=a+b$$

where $a$ and $b$ are such that

$$\left\lfloor \frac{2^a}{3^b}\right\rfloor=n \text{ and } a \text{ is minimal}.$$

We call $p(n)$ the poids of $n$.

With that being said, let's look up at what this sequence look like.

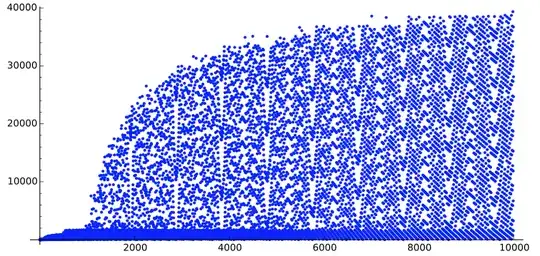
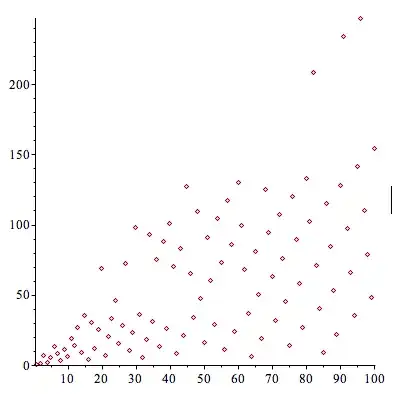
• For $n$ from $1$ to $100$:

$n$ from $1$ to $100$" />

• For $n$ from $1$ to $1000$:

From these two first graphs of the poids $p$, we can see some kind of patterns. Which seems at the same time very regular and predictable, but also a little random, with holes and extra unexpected points.

But let's look up the sequence a little further.

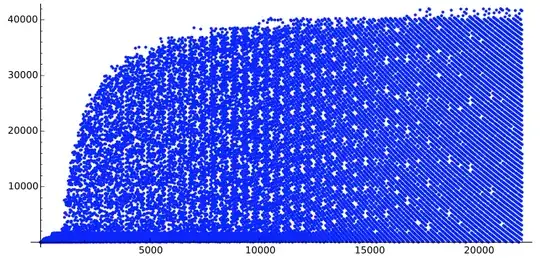
• For $n$ from $1$ to $2000$:

We now see a huge explosion of the poids around $1000$, a pattern getting more and more regular on the bottom, and apparent randomness on the top. And something which look like a gap just a little before $2000$.

We must scale down to see the big picture.

• For $n$ from $1$ to $1000$:

What a different graph. There is a pattern of waves appearing now above the initial bottom (we can clearly see the $1000$ explosion now). The wave-pattern seems to get more regular with $n$ growing.

To understand if it goes like this forever, we need to scale down even more.

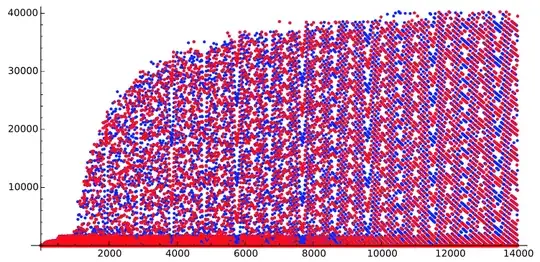
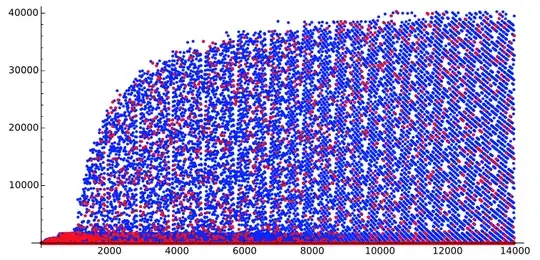
• For $n$ from $1$ to $22000$:

Now the wave-pattern is disappearing around $15000$ to another kind of pattern.

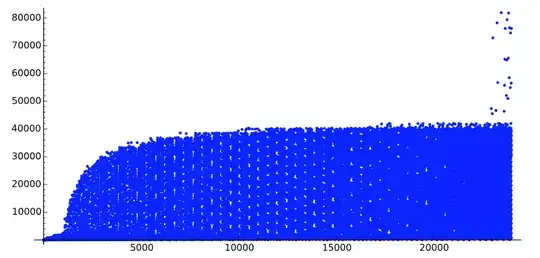
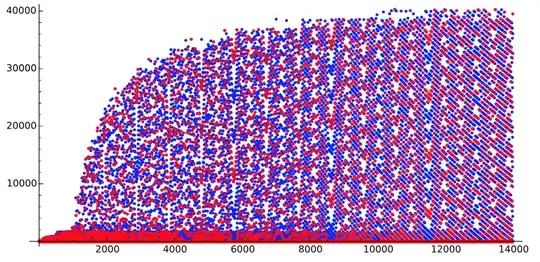
• For $n$ from $1$ to $24000$:

We have another explosion of the poids a little before $24000$.

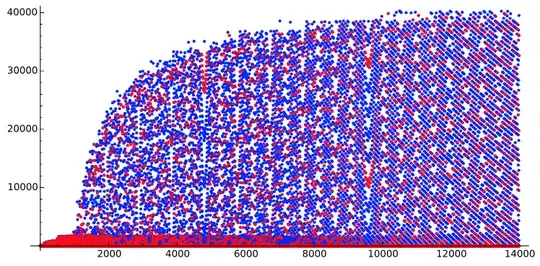
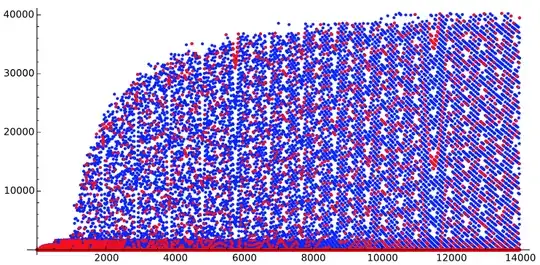
Let's go further (but don't take credit of the $x$-axis, it is wrong, my bad... I couldn't display the full picture, computation starting to get really big at this point).

• For $n$ from $24000$ to $32000$:

I have personally trouble imagining we are looking at the very same sequence at this point. We know have two layers, just like we did right after the first explosion at $1000$. A very regular layer on the bottom, and some beautiful waves on the top. The waves gaining one "wave" each time they appear.

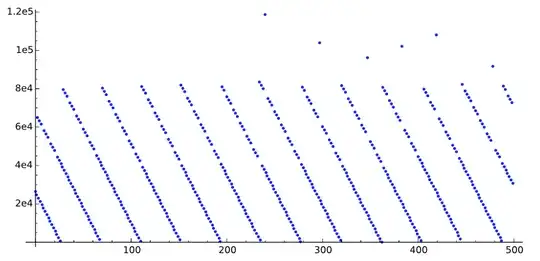
We want to look more precisely at the sequence, so we construct its values for $n\in [40000, 40500]$.

• For $n$ from $40000$ to $40500$:

Finally we highlighted the multiple of $2$, $3$, $5$, and $6$, and some interesting things can be observed. We also highlighted the prime numbers as a curiosity, but I found nothing from there.

• The multiples of $2$:

• The multiples of $3$:

• The multiples of $5$:

• The multiples of $6$:

• The prime numbers:

Well, now that we had a good look at this amazing sequence, let's try to do some maths.

Here it is what I've proven so far (not much i fear, but I can send you proofs if requested).

Theorem 1

We have

$$\forall n\geq 1,\quad \log_2(n)\le p(n).$$

Which leads to:

Corollary 1

We have

$$p(n)\xrightarrow[n\to+\infty]{} +\infty.$$

But also:

Theorem 2:

We have

$$\forall k\geq 2,\quad p(k)= \min\{p(2k)-1\ ,\ p(2k-1)-1\}.$$

I haven't actually proven the following, but i do think it's true:

Theorem 3:

We have

$$\forall k\geq 2,\quad p(k)\leq p(3k)+1.$$

I have a lot of questions about this sequence, and I hope you do to. Anything which could help understand this sequence better, and any result about it would be much appreciated.

Edit

As requested, I am going to ask some specifics questions. Though any result would be great.

I think it would be natural to have a formula of the form

$$p(n)+p(m)\leq p(nm)$$

which would be valid "most of the time". I don't succeed in producing a proof though.

I would like to know what is the function being the better upper bound (it looks like a combinaison of several logarithms).

Finally, is there a reason why the sequence is regularly "exploding" (which it does around $1\, 000$ and $23\, 000$ for instance) ?

Answer 1

I'm answering a heuristic question, so I won't go out of my way to be too precise. Roughly speaking, the explosions you are looking at have to do with the continued fraction of $\log3 / \log2$.

You're looking for the pair $(a,b)$ with minimal $a$ such that $n \leq 2^a / 3^b < n+1$. Taking logs of everything, we want $\log(n) \leq a \log 2 - b \log 3 < \log(n+1).$ There's no particular reason to restrict this to the integers; we can reparametrize with $x = \log n$ and substitute to get the inequality $x \leq a \log 2 - b \log 3 < x + \log(1 + e^{-x})$. Let's write $\varepsilon(x) = \log(1 + e^{-x})$; note that $\varepsilon(x)$ is very close to $e^{-x} = 1/n$.

So we're interested in what numbers of the form $a \log2 + b \log3$ fall into the moving and rapidly narrowing interval between $x$ and $x + \varepsilon(x)$. Some of the effects you're observing are due to the fact that the window is moving, some are due to the fact that it's narrowing, and some are due to the fact that you only plot the result when $e^x$ is an integer. If you want to isolate some of these behaviors you could, say, let the window slide continuously without narrowing.

The explosions are due to the fact that the window is narrowing. They correspond to rapid increases in the answer to the following question: given $x$, how big do we need to let $a$ to be, in order for all gaps between the values of $a\log2 + b\log3$ to be smaller $\varepsilon(x)$?

We care about size of the biggest gaps in the set $S_A = \{a\log2 + b\log3 ; a, b \in \mathbb Z, 0 \leq a < A\}$. This set is periodic with period $\log 3$, so we might as well mod out by multiples of $\log 3$: Letting $\alpha = \log3 / \log2$, we're looking a circle of circumference $\log 3$, and the subset $\widetilde S_A$ of that circle consisting of a point, the rotation of that point by $\alpha^{-1}$ of a full rotation, by $2\alpha^{-1}$ of a full rotation, and so on up until $(A-1)\alpha^{-1}$ of a full rotation. Specifically, we care how the size of the biggest gap between points of $\widetilde S_A$ depends on $A$. This displays the sort of 'jumpy' behavior where one thing happens for a while until another thing starts happening, and so on.

At first, the size of the biggest gap shrinks down from $1$ by $\alpha^{-1}$ of a full circle each time you increase $A$ by 1. But eventually at step $A_1 = \lfloor \alpha \rfloor$ you wrap around and the smallest gaps begin shrinking by $1-A_1/\alpha$ full rotations instead, and it takes $A_1$ steps to shrink them all. Eventually you suffer another slowdown, and another, and so on. Note that if $\alpha$ were rational then eventually you would end up right back where you started, and the gaps would stop shrinking entirely.

You suffer a severe slowdown when you happen to hit a particularly good rational approximation $A/B$ of $\alpha$; a convergent of the continued fraction of $\alpha$. At a time like that, making $A$ rotations by $\alpha^{-1}$ brings you particularly close to an integer number $B$ full rotations around the circle, and the rate at which our gaps shrink drops to an amount of $A\alpha^{-1} - B$ full rotations every $A$ steps, and that's how big the largest gaps will be at the next slowdown.

For example in our case 1054 rotations by $\alpha^{-1}$ brings you unusually close to 665 full rotations around the circle, within $1054\alpha^{-1} - 665$ of the starting point, i.e. a distance of $s = |1054\log2 - 665\log 3| \approx 1/23000$. At this time the big gaps in $\widetilde S_A$ have size corresponding to the previous convergent: $|485\log 2 - 306\log 3| \approx 1/1000$. To actually cover the circle with gaps as short as $s$, we need to wait until we reach the next good rational approximation of $\alpha$, which is $24727/15601$. So for values of $A$ between 1054 and 24727, the biggest gap in $\widetilde S_A$ shrinks down roughly linearly from around 1/1000 to 1/23000.

That means that while $\varepsilon(x)$ remains above 1/1000 or so, the set $S_{1054}$ has elements in every interval of length $\varepsilon(x)$, and in particular, you can always find an $a$ between 0 and 1054 for which $x \leq a \log2 - b\log3 < x + \varepsilon(x)$. But as $\varepsilon(x)$ gets below 1/1000, you fairly quickly start to need larger values of $a$. By the time $\varepsilon(x)$ is as small as 1/2000 or so, $A$ needs to be halfway between 1054 and 24727 to ensure no gaps in $S_A$ of size above $\varepsilon(x)$. So you experience a rapid jump in how big $a$ needs to be when $\varepsilon(x)$ is around 1/1000, i.e. when $n$ is around 1000. When $n$ is smaller values of $a$ less than 1054 suffice, so you have $a + b = p(n)$ less than around 1700. When $n$ is larger, you rapidly start to need bigger values of $a$, giving you bigger values of $p(n)$.

More generally, if $A/B$ is a convergent of the continued fraction of $\log3 / \log2$, then you experience this explosion when $\varepsilon(x)$ gets as small as $A \log2 - B\log3$, i.e. around $n = |A \log2 - B \log 3|^{-1}$. The convergent 485/306 leads us to expect an explosion when $n$ is around 1000, and the next convergent 1054/665 leads us to expect one when $n$ is around 23000. The next explosion, corresponding to the convergent 24727/15601, will occur when $n$ is around 55000.

Heuristically, the upper bound you're looking for is one where $p$ is a piecewise linear function of $1/n$, interpolating between the explosions. Particularly big explosions will occur when you have particularly good rational approximations of $\alpha$, i.e. when you have particularly large terms in the continued fraction. The limiting case of this is when $\alpha$ turns out to be rational, in which case $p$ won't even be well-defined past a certain point. (Though of course you'd need numbers other than 2 and 3 in the definition to see this happen.)